大学物理学平面极坐标系

虽然直角坐标系是最广泛采用的坐标系，但在处理平面曲线运动时，采用平面极坐标系更为简便.取参考系上一固定点O 作极点，过极点所作的一条固定射线OA 称为极轴.过极轴作平面，并假定质点就在该平面内运动.在某时刻质点处于点P，连线OP称为点P 的极径，用ρ 表示；自OA 到OP 所转过的角θ 称为点P的极角.于是点P 的位置可用两个量（ρ，θ）来表示，这两个量就称为点P 的极坐标，如图1.6 所示.质点P 的位置矢量r（t）可以表示为

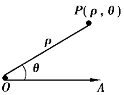
图1.6　极坐标

式中eρ（t）是极径方向的单位矢量，长度为l， 沿ρ 增大的方向.单位矢量eρ 的方向并不是固定不变的，因为随着质点的运动，点P的极角在改变，eρ 的方向也相应改变，所以eρ 的方向是时间的函数，故写为eρ（t）.

根据定义，质点的速度应表示为

式中是eρ 的方向随时间的变化率.由图1.7 可见，在Δt 时间内，质点沿任意平面曲线L 由点A 到达点B，极角的增量为Δθ.当Δt→0 时，Δeρ 的方向趋于极角增大的方向，即eθ 方向.于是下面的关系成立：

图1.7　极坐标下的运动描述(www.xing528.com)

进而得

上式的第一项是速度的径向分量，称为径向速度，第二项则是速度的横向分量，称为横向速度.这样上式也可以表示为

其中，

所以，在一般情况下速度的大小应由下式算出：