物体A和物体B的速度及加速度

一般情况，物体的速度是变化的^[1].为描述速度的变化，引入加速度的概念.

如图1.3 所示，在时刻t，质点位于点A，其速度为vA，在时刻t+Δt，质点位于点B，其速度为vB，则在时间间隔Δt 内，质点的速度增量为Δv=vB-vA.定义

图1.3　平均速度

为质点的平均加速度.它表示在单位时间内的速度的增量.一般情况下，平均加速度的大小和方向与所取时间及时间间隔的大小有关，即

用平均加速度来描述质点的运动变化快慢是粗略的.当Δt→0 时，平均加速度的极限值称为瞬时加速度，简称加速度，用a 表示，即

a 的方向是Δt→0 时Δv 的极限方向，而a 的大小是的极限值，即

在直角坐标系中，式v=vxi+vyj+vzk，加速度可以写为

或

则加速度的大小可以写成

在图1.4 中，设质点在任意两个非常靠近的位置A 和B 的速度分别为vA 和vB，将矢量vB 平移到点A，根据平行四边形定则可得到Δv.可以看出，Δv 的极限方向大致指向曲线的凹侧.所以，加速度a 的方向是大致指向曲线的凹侧的.质点在任一位置上的加速度与速度之间的夹角θ 存在下面的规律：当时，θ>π/2；当时，θ<π/2.这表明，当质点作减速运动时，加速度方向与速度方向成钝角；质点作加速运动时，加速度方向与速度方向成锐角.由此可以推断，当vA=vB 时，必定有θ=π/2，即当质点作匀速率曲线运动（速度大小不变，方向改变）时，加速度的方向与速度的方向相垂直.

在国际单位制中，加速度的单位是m·s-2（米/秒2）.

根据加速度的定义式（1.11），可得

若求质点从t0 到t 时间内速度的变化，可对上式积分，即

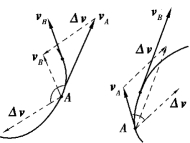
图1.4　速度与加速度(www.xing528.com)

或写成

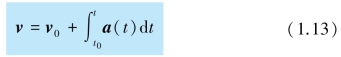
该式称为速度公式.进而可得位矢的一般表达式为

如果知道质点运动加速度与时间的函数关系，代入上式积分就可以求得位矢.

例1.1　一质点沿Ox 轴运动，坐标与时间的变化关系为x=4t-2t3，式中x、t 分别以m、s 为单位，试计算：（1）在最初2 s 内的平均速度，2 s 末的瞬时速度；（2）1 s 末到3 s 末的位移、平均速度、平均加速度，3 s 末的瞬时加速度.

解　质点沿Ox 轴做直线运动时，其位移、速度、加速度等矢量的方向都沿x 轴方向.

（1）在最初2 s 内的平均速度为

2 s 末的瞬时速度为

“-”号表示质点向Ox 轴负方向运动.

（2）1 s 末到3 s 末的位移为Δx=x3-x1=-44 m 1 s 末到3 s 末的平均速度为

“-”号表示质点向Ox 轴负方向运动.

1 s 末到3 s 末的平均加速度为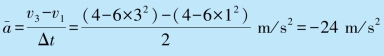

3 s 末的瞬时加速度为

“-”号表示质点的加速度指向Ox 轴负方向.

例1.2　如图1.5 所示，A、B 两物体由一长为l 的刚性细杆相连，A、B 两物体可在光滑轨道上滑行.如物体A 以恒定的速率向左滑行，当α=60°时，物体B 的速度为多少？

解　按图所选的坐标轴，物体A 的速度为

式中“-”号表示物体A 沿Ox 轴负方向运动.物体B 的速度为

图1.5　例1.2 用图

由于△OAB 为一直角三角形，故有x2+y2=l2.考虑到细杆是刚性的，其长度l 为一常量，但x、y 都是时间的函数，故有

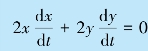
可得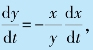于是物体B 的速度为所以有vB=v tan α，方向沿y 轴正向.当α=60°时，vB=1.73v.