演化博弈理论及模型-生态农业产业链系统管理策略研究

演化博弈论是博弈理论趋向有限理性的新发展，产生于生物学领域。演化博弈论突破了传统的完全理性假设，是分析有限理性与非理性行为的有力工具，是传统博弈论的自然拓展。演化博弈理论融合了动态演化和博弈理论，区别于传统静态分析和比较静态分析，其核心的概念有演化稳定策略ESS和复制动态概念RD。

演化博弈模型的建立基于两个方面：选择和突变。选择是指本期能够获得较高支付的策略在下期变得更为盛行；突变一般很少发生，以随机的方式选择策略，突变也要经过选择，只有好的策略才能生存下来。选择有各种可能的形成机制，这些机制可以是生态的(后代的数量)，也可以是个人的(经验、刺激反应)，还可以是社会的(学习与模仿)。好的策略会变得更为盛行，该过程是不断改进和自适应的[129]。

演化博弈的基本均衡概念—— 演化稳定策略ESS是生态学家John Maynard Smith结合生物演化论与传统博弈理论提出来的，其主要思想：一个“策略”是一种行为“表现型”，即指个体在某个自己所知的处境中将会采取的行动。演化稳定策略是这样一个策略：如果整个种群的每一个成员都采取这样一个策略，那么自然选择的作用下，不存在一个具有突变特征的策略能够侵犯整个种群[130]。系统选择演化稳定策略时所处的状态就是演化稳定状态，此时的均衡就是演化稳定均衡。

演化博弈基本概念 —— 复制者动态(RD)是生态学家Taylorand Jonker在考察生态演化现象时提出的。复制者动态是指选择某一策略数量的增长率，等于选择该策略时所得的支付与平均支付之差。复制者动态可以用基于自然选择和适应度的常微分方程描述：(www.xing528.com)

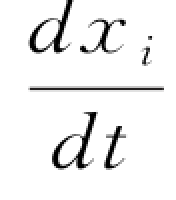=[u(si，x)-u(x，x)]xi，其中u(si，x)表示群体中选择纯策略si的个体所得到的期望支付。u(x，x)=∑xiu(si，x)表示群体平均期望支付。该式表明，如果一个选择纯策略si的个体得到的支付少于群体平均支付，那么选择纯策略si个体增长率为负；如果一个选择策略si的个体得到的支付多于群体平均支付，那么选择纯策略si的增长率为正；如果个体选择纯策略si所得到的支付等于群体平均支付，则选择纯策略si的增长率为零[131]。

在此基础上，常微分复制者动态方程的稳定性可以用来表达演化稳定策略。