SD模型探索：生态农业系统的因果回路及变量符号

系统动力学理论认为复杂系统的行为取决于系统内变量间的因果/反馈作用，系统的动态变化，如增长、衰减和振荡，都产生于两种反馈环的交互作用，即正(或自我加强的)和负(或自我调整的)反馈回路(又称“反馈环”)。因此SD 模型以反馈环来描述系统结构，建立SD模型的主要目的就是通过描绘决定系统动态变化的反馈过程、存量和流量结构、时间延迟以及非线性，帮助人们理解系统动态变化为什么会发生，向人们提供一个进行学习与政策模拟分析的工具[50]。系统动力学中使用因果关系图和存量流量图(简称“流图”)来刻画系统的结构。

(1)因果关系图(causal relationship diagram)

一张因果关系图包含多个变量，变量由因果链连接，因果链由箭头表示，每个因果链都具有极性，或者为正(+)或者为负(-)，该极性指出了当原因变量变化时，结果变量会如何随之变化(如图2.1)。

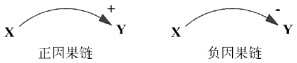
图2.1　因果链及其极性

一条正因果链意味着如果原因变量(X)增加，结果变量(Y)也会增加或X 减小引起Y 减少，即X 和Y 两个变量的变化方向相同；一条负因果链意味着如果原因变量(X)增加，结果变量(Y)就会减少或X 减少引起Y 增加，即X 和Y 两个变量的变化方向相反。

由两条或两条以上的因果链组成的回路构成因果回路(反馈环)，分为正因果回路(正反馈环)和负因果回路(负反馈环)。当回路中某个要素产生变化，通过回路的作用导致这种变化增强，称其为正反馈环；相反的，当回路中某个要素变化，通过回路的作用使这种变化减弱，则称其为负反馈环(如图2.2)，图中通常也会标出回路极性。由若干正、负因果回路构成的关系图称为因果关系图。

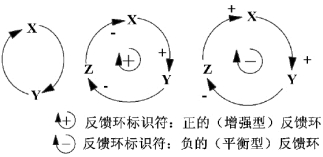
图2.2　因果回路

(2)流图(stock and flow diagram)

在社会、经济和生态系统中，存量和流量是两种最基本的变量。存量也称作流位变量(Level Variable)，是描述系统积累效应的变量，表征系统的状态并为决策和行动提供信息基础，其取值是系统在某一特定时刻物质存量积累。流率变量(Rate Variable)，反映系统积累效应的变化快慢，描述流位变量的时间变化率，流入速率与流出速率之间的差值随着时间累积而产生流位，流位只能通过其流入或流出速率而改变。当系统的物质和信息停止流动，即流率的值为零时，流位保持该时段的值。

系统动力学使用特定的绘图符号(由Jay W.Forrester在1961年创立)来描述流位和流率(图2.3)。

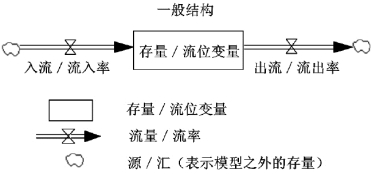
图2.3　系统动力学流图及变量符号

(3)系统动力学变量方程的规则

在流图的基础上，SD 将系统要素之间关系定量描述为一组函数式，本质上是一组微分方程。由于社会经济系统变量间的非线性作用，难以获得复杂系统的解析解，加上管理决策并非时间连续函数，所以一般求系统数值解，即将微分方程差分化，再利用计算机按照设定时间步长进行仿真分析。

SD 方程共有五类，分别是流位方程、流率方程、辅助方程、常数方程和初值方程，这五类方程在实际系统中具有各自的使用规则。

①流位方程(L)

流位变量方程是SD 的基本方程，是描述SD 模型中存量/流位变化的方程。根据流位和流率的关系，流位是流率变化对时间的积累，以积分方式来描述，流位变量方程可用如下积分形式描述[]：(www.xing528.com)

在Vensim 软件中，用INTEGRAL函数来表示这一方程：

存量/流位变量=INTEG (入流/流入率-出流/流出率，Initial value)

②流率方程(R)

流率方程是定义一个单位时间间隔(DT)内流率形式的方程，其实质是流率变化的自然规则或人为调节流位的决策干预。流率变量方程的标准形式是[]：

流位变量RAT(t)=f1[LEV(t)，A(t)，RAT1(t-Δt)

其中，LEV(t)表示等式右边含流位，应为t时刻值；

A(t)表示等式右边含辅助变量，应为t时刻值；

RAT1(t-Δt)表示等式右边含其他流率变量，应为t-Δt时刻值。

流率变量方程的确定是难点，通常根据不同的实际背景确定。例如，当流率方程描述的是自然规律时，可通过发现这一规律来构造方程；当流率方程描述的是人们调节存量的主观愿望，及决策规则时，则按决策过程构造方程。

③辅助变量(A)

辅助变量方程是为简化流率方程而设立的，因此辅助变量方程具有流率变量方程的形式，又因为在仿真计算时，辅助变量计算是在流位变量之后，在流率变量计算之前，所以辅助变量方程标准形式为[52]：

其中，LEV(t)表示等式右边含流位，应为t时刻值；

A2(t)表示等式右边含另一辅助变量，应为t时刻值；

RAT(t-Δt)表示等式右边含流率，应为t-Δt时刻值。

辅助变量之间的运行规则应根据实际意义确定，方程的建立一般采用“跟踪”法，按逻辑顺序依次构建。要注意辅助变量之间不能出现“环”，即辅助变量之间不能形成环状引用或定义，其中要有流位变量解耦。

上述三种方程是Vensim 模型中主要的变量方程，其他的如常量只需直接赋一个固定值；外生变量影响到其他系统内生变量但不受内生变量影响，所以往往是关于时间t的函数。