线性代数全解：高教社第3版习题P51

1.选择题

(1)如果=2,则=(　).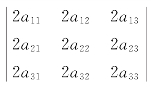

(A)2　(B)4　(C)12　(D)16

(2)已知4阶方阵A,其第三列元分别为1,3,-2,2,它们的余子式的值分别为3,-2,1,1,则行列式|A|=(　).

(A)5　(B)-5　(C)-3　(D)3

解题指导:(1)是考查对行列式性质“用一个数k乘以行列式的某一行(列)的各元素,等于该数乘以此行列式”;(2)是考查对行列式展开定理“行列式等于它的任一行(列)的所有元素分别与它们所对应的代数余子式的乘积之和”的理解与掌握.另外,要注意(2)中告诉的是余子式而非代数余子式,在利用展开定理计算行列式时要添上符号,变成代数余子式.

解　(1)选D.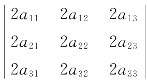=23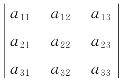=23×2=16.

(2)选A.|A|=1×(-1)1+3×3+3×(-1)2+3×(-2)+(-2)×(-1)3+3×1+2×(-1)4+3×1=5.

2.设|A|=,则A31+A32+A33=________;A34+A35=________.

解题指导:此类题目一般不宜算出表达式里每一项的值,而是注意观察要求的表达式的结构,充分利用按行(列)展开的计算方法来进行巧妙计算.

解　3(A31+A32+A33)+2(A34+A35)==0(第三行,第四行相同),

即　

同理　

于是　

故答案为0,0.

3.计算下列行列式.

(1);

(2);

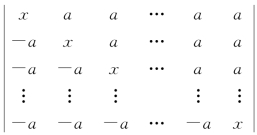(3).

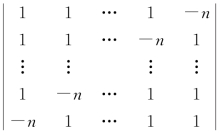解　(1)从第n行开始,前一行乘(-1)加到后一行,再将第一列乘以(-1)加到其他各列,则(www.xing528.com)

原式==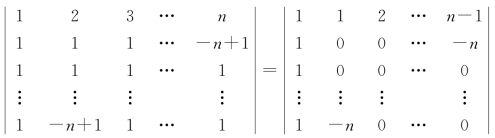

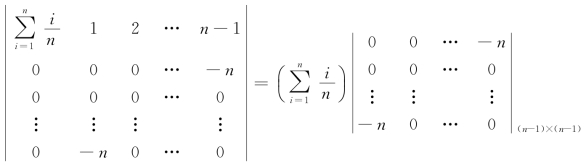
(2)记原行列式为Dn,利用拆行列式法,x=(x-a)+a,将第n列拆开,则

(右边第一个行列式按最后一列展开,第二个行列式最后一列加到其余各列)

同理,由Dn=DnT得Dn=(x+a)Dn-1+(-a)(x-a)n-1.

以上两式联立解方程组得.

(3)分别将第二行到第n行加到第一行,

原式=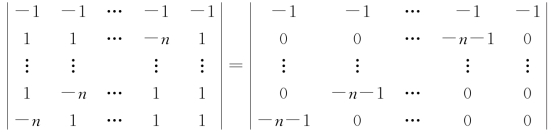

4.证明

解　D1=cosα,D2=cos2α,要证明Dn=cosnα.

对阶数用第二数学归纳法证明.

n=1,2时,结论成立.假设对阶数小于n时,结论成立,将n阶行列式按第n行展开,有

5.某电器公司销售三种电器,其销售原则是,每种电器10台以下不打折,10台及10台以上打9.5折,20台及20台以上打9折,有三家公司来采购电器,其数量与总价见下表:

问各电器原价为多少?

解　设甲、乙、丙三种电器的原价分别为x,y,z元,由题意可得

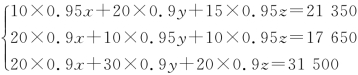,解得.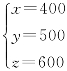

6.问λ,μ为何值时,齐次线性方程组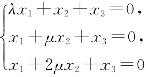有非零解?

解题指导:如果齐次线性方程组有非零解,则其系数行列式一定为零.

解　D=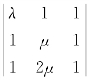=μ-μλ,齐次线性方程组有非零解,则D=0,即μ-μλ=0,得μ=0或λ=1.不难验证,当μ=0或λ=1时,该齐次线性方程组确有非零解.