线性代数同步辅导与习题全解：五总完整答案

1.将矩阵化成行最简形矩阵.(请读者注意本题的结果.)

解　

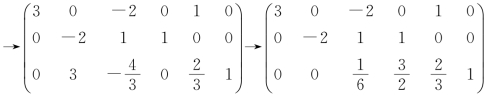
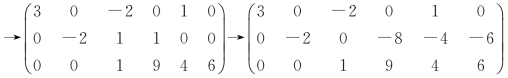
注:本题所得到的行最简形矩阵与原矩阵具有某种类似“对称性”的特点.

形如(A┊I)～(I┊A-1)是求逆阵的常用做法,参考教材第91页.

2.(物资调运问题)有三个生产同一产品的工厂A1,A2,A3,其年产量分别为40t,20t和10t,该产品每年有两个用户B1和B2,其用量分别为45t和25t,由各产地Ai到各用户Bj的距离为Cij(km)如表1-1所示(i=1,2,3;j=1,2),不妨假设每吨货物每千米的费用为1元,问各厂产品如何调配才能使总费用最少?

表1-1

解　假设各厂运到各用户的产品数量如表1-2所示.

表1-2

则总运费为S=45x1+58x2+92x3+58x4+72x5+36x6,且

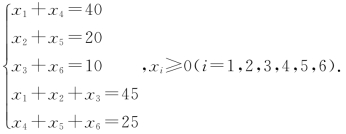
→,故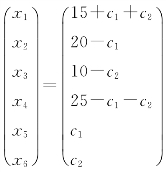(c1,c2为任意常数),代入S表达式,有

由于c1,c2分别是x5,x6的值,则

显然,当c1=0,c2=10时,S最小.此时

3.λ取何值时,非齐次线性方程组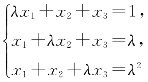

(1)有唯一解;(2)无解;(3)有无穷多解.

解题指导:先利用矩阵的行初等变换,将线性方程组所对应的增广矩阵化成行阶梯形矩阵,然后根据线性方程组有解的要求来讨论未知参数的取值.另外,在对含参数的矩阵作初等变换时,含参变量的式子一般不宜作分母.若作分母,则使分母为零的参数值需另行讨论.

解　对方程组的增广矩阵进行初等行变换化为行阶梯形矩阵,得

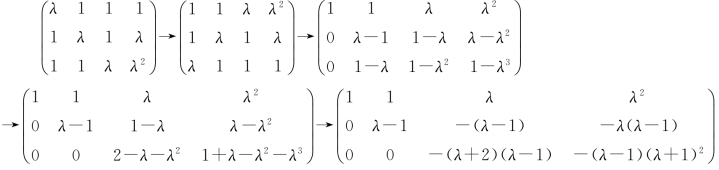
(1)当λ≠1且λ≠-2时,方程组有唯一解;

(2)当λ=-2时,方程组无解;

(3)当λ=1时,方程组有无穷多解.

4.对于线性方程组

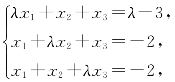
问当λ为何值时,方程组无解?有唯一解?有无穷多解?(www.xing528.com)

解题指导:本题与第3题属于同一种题型,解题的思路、方法也类似.

解　对方程组的增广矩阵进行初等行变换化为行阶梯形矩阵,得

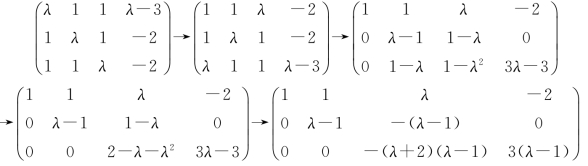
(1)当λ=-2时,方程组无解;

(2)当λ≠1且λ≠-2时,方程组有唯一解;

(3)当λ=1时,方程组有无穷多解.

5.对于给定的三个线性方程组(Ⅰ)、(Ⅱ)、(Ⅲ),证明:

(1)若方程组(Ⅱ)是方程组(Ⅰ)的线性组合,方程组(Ⅲ)是方程组(Ⅱ)的线性组合,则方程组(Ⅲ)是方程组(Ⅰ)的线性组合.

(2)若方程组(Ⅰ)与方程组(Ⅱ)等价,方程组(Ⅱ)与方程组(Ⅲ)等价,则方程组(Ⅰ)与方程组(Ⅲ)等价.

解题指导:(1)利用线性组合的概念,将某个方程组表示成另一个方程组的线性组合,然后代入整理即可证明;(2)利用(1)的结果,结合方程组等价的概念,容易证明.

证明　(1)为了不失一般性,不妨设三个方程组为以下形式

方程组(Ⅰ)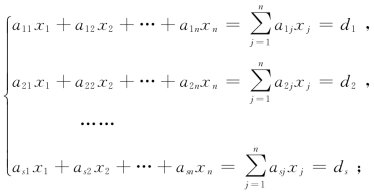

方程组(Ⅱ)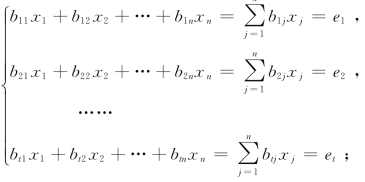

方程组(Ⅲ)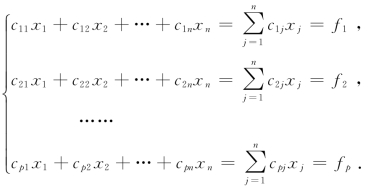

根据题意,若方程组(Ⅱ)是方程组(Ⅰ)的线性组合,那么方程组(Ⅱ)中的每一个方程都可以由方程组(Ⅰ)中的方程线性组合表示.

任取一个bi1x1+bi2x2+…+binxn=ei(i=1,2,…,t).

左边加和得,

右边加和得,(kir为组合系数).

同理,方程组(Ⅲ)是方程组(Ⅱ)的线性组合,那么方程组(Ⅲ)中的每一个方程都可以由方程组(Ⅱ)中的方程线性组合表示.

任取一个ci1x1+ci2x2+…+cinxn=fi(i=1,2,…,p).

左边加和得,

右边加和得,(lij为组合系数).

则左边为

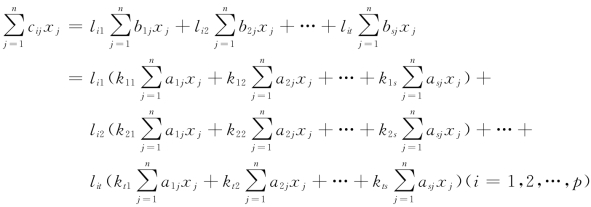
右边为

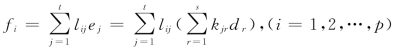
即方程组(Ⅲ)中的任一方程均可由方程组(Ⅰ)中的方程线性组合表示.

因此,方程组(Ⅲ)是方程组(Ⅰ)的线性组合.

(2)若方程组(Ⅰ)与方程组(Ⅱ)等价,则方程组(Ⅰ)与方程组(Ⅱ)互为线性组合;方程组(Ⅱ)与方程组(Ⅲ)等价,则方程组(Ⅱ)与方程组(Ⅲ)互为线性组合.

由(1)的证明过程可以证明,方程组(Ⅲ)是方程组(Ⅰ)的线性组合,同时,方程组(Ⅰ)也是方程组(Ⅲ)的线性组合.

因此,方程组(Ⅰ)与方程组(Ⅲ)等价.