消元法求解线性方程组

1.消元法求解线性方程组

消元法的基本思想是通过方程组的同解变形,使各方程中所含未知量的个数依次减少,把方程组化为容易求解的同解方程组,从而达到求解的目的.用消元法求解线性方程组的具体做法就是对方程组反复进行以下三种变换:

(1)交换两个方程的次序;

(2)用一个非零的常数乘某个方程;

(3)把一个方程的适当倍数加到另一个方程上.

以上这三种变换称为线性方程组的初等变换.可以证明:线性方程组的初等变换是将方程组化为同解方程组.

例1　解线性方程组

解题指导:利用方程组的同解变换,先消元,再回代.

解　将方程组①中第1个方程的(-2)倍、(+1)倍和(-4)倍分别加到第2、第3、第4个方程上,消去这三个方程中的未知量x1,得

将方程组②中第2个方程的(+1)倍和(-1)倍分别加到第3和第4个方程上,消去这两个方程中的未知量x2;这时第3个方程两边全为零,即为恒等式,交换第3、第4个方程,得

显然,方程组③中的第4个方程多余,去掉该方程;并将方程组③中的第3个方程两边乘以,得

从方程组④的第3个方程可得x3=2,将x3=2依次代入前2个方程(也就是把第3个方程的适当倍数分别加到前两个方程上,消去这两个方程中的x3),得

将方程组⑤中的第2个方程两边乘以,得

将方程组⑥中的第2个方程的(-1)倍加到第1个方程上,得

显然,方程组①～⑦都是同解方程组,故方程组⑦的解即为原方程组的解.

思路总结:在上述求解过程中,①～③称为消元过程,④～⑦称为回代过程,形如③式的方程组称为阶梯(形)方程组.消元法的思想就是利用方程组的初等变换将原方程组化为阶梯(形)方程组,而这个阶梯(形)方程组与原线性方程组同解,解这个阶梯(形)方程组即可求得原方程组的解.

2.矩阵的初等变换

对矩阵作如下三种变换称为矩阵的初等行变换:

(1)对调矩阵的任意两行(对调第i,j两行,记作ri↔rj);

(2)以非零常数k乘矩阵某一行的各元(第i行乘k,记作ri×k);

(3)把某一行所有的元的k倍加到另一行对应的元上(第j行的k倍加到第i行上,记作ri+krj).

把定义中的“行”换成“列”,即得初等列变换的定义(所用记号是把“r”换成“c”).矩阵的初等行变换与矩阵的初等列变换统称为矩阵的初等变换.

注意:(1)矩阵的三种初等变换都是可逆的;

(2)若矩阵A经过有限次初等行变换变成B,则称A与B行等价,记作A～B;若矩阵A经过有限次初等列变换变成B,则称A与B列等价,记作A～B;若矩阵A经过有限次初等变换变成B,则称A与B等价,记作A～B.等价关系具有以下性质:

(ⅰ)自反性　A～A;

(ⅱ)对称性　若A～B,则B～A;

(ⅲ)传递性　若A～B,B～C,则A～C.

数学中把具有上述三条性质的关系称为等价关系.例如,两个线性方程组同解,就称这两个线性方程组等价.

例2　试用初等变换将矩阵化为行阶梯形.

解　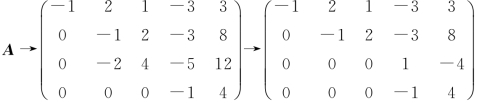,矩阵B1即为行阶梯形矩阵.

若将B1再作初等行变换,则化为如下形状

其中B2称为行最简形矩阵,其特点是非零行的第一个非零元为1,且这些非零元所在列的其他元全为零.

注意:(1)用数学归纳法可以证明,任何一个矩阵Am×n,都可以经过有限次初等行变换化为行阶梯形矩阵和行最简形矩阵.

(2)再经过初等列变换,B1或B2可化为

矩阵F称为矩阵A的标准形,其特点是F的左上角为一个单位矩阵,其他元全为零.

(3)一般地,对m×n矩阵A,可以通过初等变换(行变换和列变换)化为下面的标准形(www.xing528.com)

此标准形由m,n,r三个数完全确定,其中r就是行阶梯形矩阵中非零行的行数.

3.利用矩阵的初等变换求解线性方程组

对于一般的线性方程组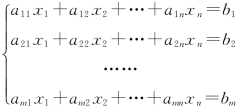,有三种可能情况:无解,有唯一解或有无穷多个解.也就是说,对于任意一个线性方程组,其求解的结果必然为这三种情况之一.

而对于一般的齐次线性方程组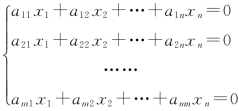,恒有解,因为它至少有零解.当然,也可能有非零解.

在具体求解线性方程组时,对其增广矩阵(A,b)进行初等行变换化为行阶梯形矩阵即可判断线性方程组解的情况,将行阶梯形矩阵进一步化为行最简形矩阵,即可得到方程组的一般解.

例3　求解齐次线性方程组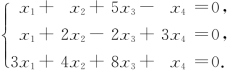

解题指导:齐次线性方程组一定有解,只需要注意它是否有非零解,不用考虑无解的情况.

解　将系数矩阵A化为行最简形矩阵

由此得出同解方程组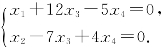

取x3,x4作为自由未知量,得

令x3=c1,x4=c2,则原方程组的解为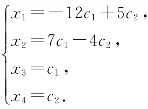(c1,c2为任意实数)

例4　求解非齐次线性方程组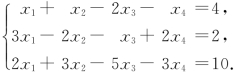

解题指导:对于非齐次线性方程组,在对增广矩阵作初等行变换时,一旦发现有无解的方程,就不用再化简了.

解　对增广矩阵作初等行变换化为行阶梯形矩阵.

（Ab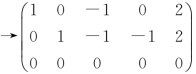）=.方程组有无穷多解.

同解方程组为(x3,x4为自由未知量)

令x3=c1,x4=c2,原方程组的解为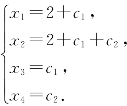(c1,c2为任意实数)

例5　λ取何值时,线性方程组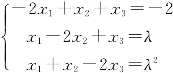有解?并求出它的解.

解题指导:先利用矩阵的行初等变换,将线性方程组所对应的增广矩阵化成行阶梯形矩阵,然后根据线性方程组有解的要求来讨论未知参数的取值.另外,在对含参数的矩阵作初等变换时,含参变量的式子一般不宜作分母.若作分母,则使分母为零的参数值需另行讨论.

解　对方程组的增广矩阵进行初等行变换化为行阶梯形矩阵,得

要使方程组有解,则需满足(λ-1)(λ+2)=0,故可得λ=1或λ=-2,此时方程组有无穷多解.

当λ=1时,(A,b)→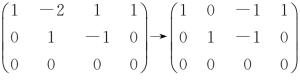

得到方程组的一般解为或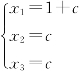(c为任意常数);

当λ=-2时,(A,b)→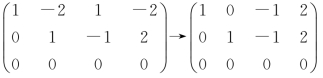

方程组的一般解为或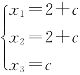(c为任意常数).

例6　a,b取何值时,下面的方程组无解、有唯一解或有无穷多个解?在有解时,求出方程组的全部解.

解题指导:先利用矩阵的行初等变换,将线性方程组所对应的增广矩阵化成行阶梯形矩阵,然后根据线性方程组有解的要求来讨论未知参数的取值.对于像本题这样含有两个未知参数的线性方程组,要综合考虑当两个参数取不同值时,线性方程组解面临的不同情况.

解　对方程组的增广矩阵进行初等行变换化为行阶梯矩阵,得

(1)当a≠-1时,有唯一解.由于a+1≠0,可将(A,b)继续化为行最简形矩阵,即

所以,当a≠-1时,原方程组有唯一解,为

(2)当a=-1且b≠0时,原方程组无解.

(3)当a=-1且b=0时,有无穷多个解.此时将(A,b)继续化为行最简形矩阵,有

所以,原方程组的一般解为,x3和x4为自由未知量.

令x3=c1,x4=c2,则原方程组的解为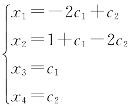(c1,c2为任意常数).