数学模型建模方法应用案例

1．问题与分析

某学校规定，某个专业的学生毕业时必须至少学习某些门类课程中的课程，同时规定了各门课程的先修关系、不能同时选修的课程要求，以及所需要的最少学分总数等要求．现在给出所有可以选修的具体课程，每门课程都有相应的学分．试建立数学模型确定一个学生若要正常毕业，应当如何选修课程，既能满足这些要求又使学习的课程数最少？

这个问题实际上就是选择问题，从所给的课程中选择某些课程，使符合要求．那么如何表示选择的课程，并且对它们的特征进行量化分析呢？这就需要对相应的课程进行量化，首先课程有学分数，我们可以给每个课程一个符号名称，但是它们不能参与直接的计算，因此引入0-1变量来表示课程是否被选上．

2．模型假设

（1）课程数记为z．

（2）总学分数为w．

（3）Sj表示第j类课程，j=1，2，…，m．

（4）aj表示Sj类课程中课程门数，j=1，2，…，m．

（5）sjk表示第j类课程中的第k门课程，j=1，2，…，m；k=1，2，…，aj．

（6）cjk表示第j类课程中的第k门课程的学分数，j=1，2，…，m；k=1，2，…，aj．

（7）bj表示第Sj类课程中需要选的课程最少门数，j=1，2，…，m．

（8）总的课程门数记为a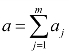，，j=1，2，…，m．

（9）j=1,2,…,m；k=1,2,…,aj．

3．模型建立与计算

（1）各类课程门数限制：第Sj类课程中需要选修的最少课程数的限制为(www.xing528.com)

（2）先修课程的关系限制：课程sj1k1是sj2k2的先修课程，则其对应的0-1变量满足关系：

xj1k1≥xj2k2

课程sj1k1是sj2k2和课程sj3k3的先修课程，则其对应的0-1变量满足关系：

xj1k1≥xj2k2，xj1k1≥xj3k3

这两个关系等价于

2xj1k1≥xj2k2+xj3k3

（3）同时选修课程的限制要求：若课程sj4k4和sj5k5不能同时选修，则需要满足

xj4k4+xj5k5≤1

（4）学分总数的要求：要求所选课程的总学分数最少是f，则有

（5）最少课程的优化模型：

可以编写LINGO程序进行计算，在此不再赘述．

4．建模方法点评

建立每门课程的0-1变量模型，相当于对每门课程上贴上0-1标签，然后根据问题的要求利用0-1变量来表示课程的门数限制、各种学分要求等．0-1变量的和是多少，就表示是有几个1，就表示选择了多少门课程；用每门课程的学分数乘以对应的0-1变量，得到这门课程的实际学分，从而得到实际选择的课程的学分，进而得到满足某些类型或者某些模块的学分要求的课程．另外，课程选择的先后顺序，也可以用课程的标示数来体现，先修课程的0-1数不能小于后选的课程，这样的基本关系可以进行等价的不等式变形，获得简洁统一的计算模型，从而通过不等式表现出全部的课程关系．

因此，在这种从多个对象中选择部分进行组合搭配，并从中选择理想结果的优化问题，可以引入0-1变量进行选择、分析、表达、计算．