1．问题与分析
今有4种资产（股票、债券、期货、信用资产）Si（i=1，2，3，4），供投资者选择，某公司现有数额为M的大资金用作一个时期的投资．对几种资产进行的评估结果是购买Si的平均收益是ri，并预测购买Si的风险损失率是qi，最后进行评估时，总的风险可以用几种资产风险率的最大值进行控制．
另外，购买Si的交易费为pi，并且购买不超过ui时，交易费按购买ui进行计算．同期存款利率是r0．给该公司设计一个投资组合方案，使净收益最大，而总体风险最小．
本模型是一个双目标最优化模型．不同的选择体现了总资金不同方式的划分，从而对应为不同的数值，进而对应于相应的变量．选择的标准是不同方案的净收益数额．因而这是一个数学规划问题，面临着对某些变量的取值过程的不同选择．
2．模型假设
（1）引入优化分析和表示中的必要数据的统一表示：以xi表示存入银行和购买Si的金额．
（2）另外，引入具有极为重要的表示某种状态是否存在的标志性变量（0-1变量）：
利用yj的取值关系和大小规律来直接表现各种购买状态的组合，这个可以利用这几个0-1变量满足的各种可能的方程或不等式的解来表示，从而为优化组合选择提供必要的数量形式．(www.xing528.com)
（3）收益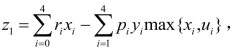
本来的表示是z1=z1（x0，…，x4），并且当xi=0时，没有手续费，因为仅用max{xi，ui}无法表示所有费用的数值组合，所以需在max{xi，ui}的前面加上系数yi，这个系数的取值由xi取值决定．
3．模型建立与计算
建立优化数学模型：
该问题属于多目标规划问题，可以用线性加权方法求解．权重的选择依据投资人的性格决定：稳健的投资人应使风险的权重系数较小；对于喜欢冒风险的投资人，应使风险权重系数更大一些．
4．建模方法点评
这些约束的实质是反映了在一次决策状况下的全部数据xi，yi，M，qi，ri，ui各自的取值范围大小、取值的变化规律、取值的运算特征与规律即不变性或具体状况、取值的差异大小、取值的阶段性与多样性、取值的环境即是否作为某种量的最大或最小、不同变量的取值相互之间的运算关系、特殊状态的关系等．为了获得这些关系，就需要想象出它们潜在的所有可能的取值组合．
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
