整数规划模型及其求解方法

在数学规划问题中，如果限制决策变量的取值是整数，则得到整数规划模型．

整数规划问题表面上似乎可以用穷举的方法进行，但是对于规模稍大的问题是不可行的，因为所有整数的组合数目太大．一种自然的想法是设法只检查一部分少数取值组合，然后进行对比分析，即分支定界法．

分支定界法的基本步骤如下：

（1）将原来的问题称为问题A，将其中的整数限制去掉，形成了一般的线性规划问题，称为与A相应的线性规划问题B．

（2）求解问题B：如果无可行解，则原问题也没有可行解；如果B有最优解，并且是整数解，符合A的条件要求，则此解就是A的最优解；如果B有最优解，但是有的变量的取值不是整数，这时记最优解的值为．

（3）用观察法找到A的一个可行解，一般可取xj=0，j=1，2，…，n，记其目标函数值为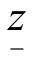，则问题A的最优函数值z*满足．这一步给出了最优解的近似值，如果这时区间的长度很小，则可求得最优值较好的近似值；如果最优解中只有极少部分的变量不取整数，那么就取与这几个变量的解相近的几个整数，组成若干个可行解，计算它们的目标函数取值，通过比较获得较好近似的最优解．因为此时的目标函数值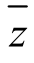已经很小（或很大）了，因此整数限制下的最优取值在此点附近（目标函数是连续的）．但是这种方法毕竟是近似的，若我们希望获得精确的最优解，则要进行下面的迭代：(www.xing528.com)

步骤1　分支．首先在B的最优解中任选一个不符合整数条件的变量xi，其值为bi，构造两个约束条件：

然后将这两个约束条件分别加入问题B，求解两个后继规划问题B1和B2．最后定界，即求出到目前为止所有分支后所得最优目标函数值的最大者作为新的上界，显然它是减少的；同时在满足整数条件要求的分支中，找出目标函数的最大者作为新的下界．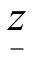

步骤2　比较与剪支．各分支的最优函数值中若有小于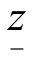者，则剪掉该支，因为从其中已无法找到更好的解．若大于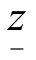，且不符合整数条件，则重复第一步．一直到不能改进，即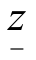=z为止，这时便得到了最优解．

分支定界法既适合于求解纯整数规划问题，同时也适合求解混合整数规划问题．它的主要思想就是，首先扩大搜索范围，使可解性比较强；如果最优解中有不合适的解，就从这个解的附近去寻找，或者再划块来分别寻找，实际上就是把原来的寻找范围进行划分，再扩大各自的寻找范围，最后对结果的大小进行比较分析．