多目标规划问题的一般形式为
通过引入向量集的优化问题如有效点（最小向量）、弱有效点（弱最小向量），引入Pareto（帕累托）最优解的概念，它能较好地反映多目标对象的大小比较是求解多目标规划的基本理论基础．
1）理想点法
首先求每个单目标规划的最优解：
，最优值为
，称
为原问题的理想点．这里的D表示决策变量x的可行区域．即使求不到最优解，我们可以去求与最优解最接近的解，因此可以构造评价函数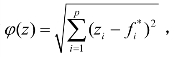
求解问题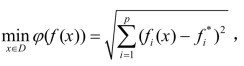
所求出的最优解可以作为Pareto意义下的最优解．
2）线性加权法
对于多目标问题，我们希望所有目标都达到最优解．如果确实达不到，那就要有所侧重，首先让某些我们认为重要的目标达到相对最大值，通过构造加权变量，使重要目标的权重增大，从而在加权变量达到最大值时，重要目标也就达到了相当大的程度．权重的选择有时要客观，有时也可用专家调查的方式获得，确切的方法可用调查比例的方式来大致确定．
构造如下形式的评价函数：令
称之为权向量集．令(www.xing528.com)
再求解
可见，这种处理方法就是将多目标问题转化成单目标问题，利用单目标达到最大值时使目标向量也达到相对优化的程度，并且照顾了特别的目标．
3）极大极小法
极大极小法的思想：要求目标向量集的极小状态，理想状况是每个分量都达到最小值，但实际是做不到的，我们的一个最基本的思想是求接近于这个状态的解，即近似解．现在找一个标准，使这个解比另外一个“小”，于是可以考虑每一个目标向量函数在决策变量取定以后，各个分量的最大值偏小，这说明这个向量状态总体上是偏小的，因此显得较优．但问题是这个标准也有很大的漏洞，因为有可能只进行最大值的比较，显得较优，而其他的分量都较大，因此不是最优解（可以考虑用第二最大值来进行比较分析）．
作评价函数：
，然后求解：
将它的最优解作为多目标规划问题意义下的最优解．
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
