治愈者免疫力的病例3传染病微分方程模型

1．问题与分析

对人群总体进行分类：易感染的人s（t），染病且能够传染的患者比例数i（t），单位时间内经过治愈的人占总人数的比例r（t），这些人属于具有免疫力不会再受到感染的人以及治疗无效死亡的人．这里的模型与案例2中的模型的差别在于，治愈的患者不再是易感染者，从而每天的易感染者人数在减少．这样的分析方法体现的模型更加符合实际，影响新增患者人数的来源也会变化，从而可建立新的不同的数学模型．

2．模型假设

同案例2的假设．

3．模型建立与计算

1）患者数量变化模型

患者数量变化模型：

每天感染患者人数的变化仍是新增加的人数减去治愈的人数，新增加的患者是感染患者传播的，主要由那些没有隔离的患者传播的．

2）易感染者人数减少模型

易感染者人数减少模型：

表示正常且可以感染的人在减少，当天减少的数量就是当天所有的被当前患者感染的人数λsi．

3）治愈后移出感染者系统的人数变化模型

治愈后移出感染者系统的人数变化模型：

治愈的数量增加值就是当天所有患者的数量与治愈率的乘积．

4）总平衡模型

总平衡模型为

i(t)+s(t)+r(t)=1

因此3个方程的方程组可以化为

进一步关注i（t），s（t）的关系为

软件计算：可以利用MATLAB编程计算求出方程组的数值解．

几何分析：可以进行相轨线分析，即建立两个因变量i-s之间的关系，分析二者相互依赖的变化规律．根据一阶微分方程的计算方法，我们求出(www.xing528.com)

根据上述关系，以及其他的关系和特征，分析出各个变量的变化趋势和特征，以及变量之间的相互关系，包括单调性和有界性等．

在区域D={（s，i）|s≥0，i≥0，s+i≤1}中分析相轨线i-s的变化规律和趋势，可以研究曲线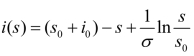的形状特征．

下面我们根据各个变量的导数及二阶导数的特点，分析各个变量的变化趋势．

（1）分析易感染者、患者人数、移出者随时间的变化趋势，即求随时间的无限增加的极限．

由于根据单调有界变量极限必存在可知，存在有限值；而且r＜1，因此也存在有限值；再根据s（t）+i（t）+r（t）=1知，也是存在的．这就证明了在当前的环境下，当时间无限延长时，3个变量都存在有限的极限．

直观分析，患者人数的极限应该是0．理论证明如下。

如果，根据有

则必有当t充分大时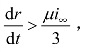，所以

所以，这与矛盾．

因此，这种情形表明，只要治愈者不再感染，患者最后会全部治愈．

（2）计算最终剩下的易感染者的比例．在关系式

中，让时间趋向于无穷大，得到

此方程的根s∞就是最终的易感染者的比例．

（3）进一步分析i（t），s（t）的具体变化规律．在分析i（t），s（t）的变化规律时，一般需要用到这些变量的单调性，实际上就是分析其导数的正负状况．函数i（t）的变化过程如下。

由

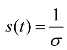可知，如果初始时刻有σs0＞1，则开始阶段必有，但是s（t）是单调减小的，因此在时刻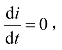，这就意味着此时刻，患者人数达到最大值，然后开始减少，最后趋向于0．

如果初始时刻就有σs0＜1，由于s（t）是单调减小的，总有因此i（t）从一开始就是单调减小的．

（4）阈值分析．从上述结果中可以看出，是一个关键数据，当初始的易感染人数使时，患者人数就会增加，呈现蔓延状态，反之就不会蔓延．因此要减轻蔓延程度，则应考虑增大阈值，就是减小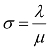，因此需要减少患者接触易感染者的人数λ，增大治愈率μ．这与直观分析结果是一致的．

4．建模方法点评

当考虑了治愈移出以后，健康人且再次被感染的总人数是减少的，通过关系式i（t）+s（t）+r（t）=1可以看出，当前时刻r（t）增大时，i（t）+s（t）就会减少，r（t）的增加数量就是当前时刻治好的患者数，即有；而此时患者人数的改变即为当前患者接触传染的数量减去治愈后移出的数量，即有，这就给出了当前时刻单位时间内这几个变量的变化规律和相互间的关系，从而建立起相应的微分方程数学模型．