易感染者与患者分布的传染病模型案例

1．问题与分析

根据传染病的传播规律，建立随时间变化的患者人数的规律，并根据这个规律进行预测分析，提出阻止传染蔓延的方法手段．

2．模型假设

（1）在时刻t，人群中易感染者占总人数的百分比为s（t），这里易感染者指的是正常人可以被感染，并且如果感染后症状非常明显，可确诊为患者．

（2）i（t）表示在时刻t，已经感染的患者人数占总人数的百分比，这里的患者已经感染病毒，有的住院隔离，有的携带病毒但没有症状，有的症状较轻等．

（3）假设每个患者每天的平均接触人数为λ，一定情形下可以假设是个常数．

（4）假设人群的总数是N且不变，这样的系统就是一个封闭的系统，在一定的时间和区域内实行了与外界的封闭隔离措施，使没有新来的人群加入．

3．模型建立与计算(www.xing528.com)

分析计算单位时间内患者数量的变化规律．用记录数据Ni（t）的导数表示这个量，再分析这个量的来源或相关数量关系．现在假设每个患者每天平均接触的人数为λ，则每天可以使λs（t）个人感染病毒，成为患者．由于患者人数为Ni（t），因此每天被这些患者接触而感染病毒的患者人数比例的变化为

即

上述方程的解为

通过计算可以知道，当时，导数达到最大值，此时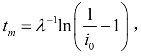这个时刻意味着增加的速度最大，门诊量最大；同时可以看到，传染程度的标志数λ影响了这个时刻，λ越大则tm越小，传染高潮来临越早．另外，从这个模型可以看到，t→∞时，i→1，这也是不合常理的．实际上传染率i应该是越来越小的，因为在总人数不变的前提下，可能受到感染的对象总数随着患者数量的增加而减少．因此该模型需要进行改进，以使更加符合实际情况．

4．建模方法点评

根据患者数量变化的规律，利用患者人数的记录数据i（t），通过自身计算得到单位时间内患者人数的变化值；再利用（λs）Ni计算当前患者单位时间内传染产生的新患者人数，然后建立二者的相等关系，得到微分方程模型．