《画法几何与阴影透视》-全面解析点的透视规律

点作为最基本的空间几何元素，讨论它的规律可以获知透视图作为中心投影的特殊法则。与正投影法需要同时获知至少两面投影方能确定点的空间位置一样，在透视投影中，点的位置需要同时由其透视与基透视共同确定。

规律1：点的透视与其基透视位于同一铅垂线上。

如图10.5所示，空间A点与其基点a的连线Aa垂直于基面G。将连线Aa与其线外S点（即视点）组成一平面，该平面容纳了包括过A点及a点所作视线在内的所有通过Aa线上任一点的视线，故可称为过Aa线的视平面。由于Aa⊥G，故该视平面也⊥G，此视平面与画面的交线自然也是垂直于G的了。

规律2：点的基透视是判别空间点的位置的依据。

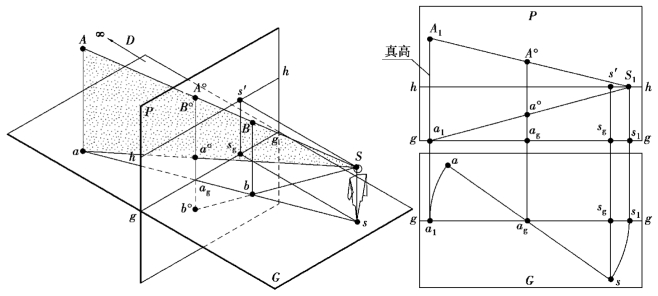
图10.5　点的透视规律及作图

图10.5中，B点与A点在空间位于同一视线上。事实上，类似于B而与A处于同一视线上的点还有无穷多。按点的透视定义，它们具有完全相同的透视。由此可见，仅仅根据某点的透视，是无法确定其空间位置的。但是，如果注意到这些点的基点及其透视（基透视）便会发现：当点位于画面之后时（如A点），其基透视在基线g—g之上方；当点位于画面之前（即人与画面之间，如B点）时，其基透视在基线g—g之下方。

规律2的三个有意义的推论如下：

①当点位于画面前时，其基透视必在基线下方。(www.xing528.com)

②当点位于画面上时，其基透视应在基线上。

③当点离开画面无穷远时，其基透视及透视均在视平面上。

规律3：点的基透视是确定空间点透视高度的起点。

如果空间点到基面的距离（即点的高度）被透视以后称为透视高度，则该透视高度就是点的透视与其基透视之间的垂直距离。若将点的基透视看成已知的，则点的透视高度便可以其基透视为起点而垂直向上量取。利用此规律可以获得后续直线规律中的真高线概念，并以真高线为基础，在已有点的基透视的情况下求出其透视。

观察点的基透视位置，可以产生的推论为：

①当空间点位于画面前时，其透视高大于真高。

②当空间点位于画面上时，其透视高等于真高。

③当空间点位于无穷远时，其透视高等于零。