《画法几何与阴影透视》-平面图形的阴影技巧

1）平面多边形的落影概念及作图

①平面多边形的落影概念：平面多边形的影线，就是被平面多边形遮挡住的光线形成的光柱体与承影面的交线。

②平面多边形影线的作图：平面多边形影线的作图，就是求出平面多边形各边线落影所构成的外轮廓线。作图时首先作出多边形各顶点的落影，再按原图形各顶点的顺序用直线依次相连，即得到多边形的落影。

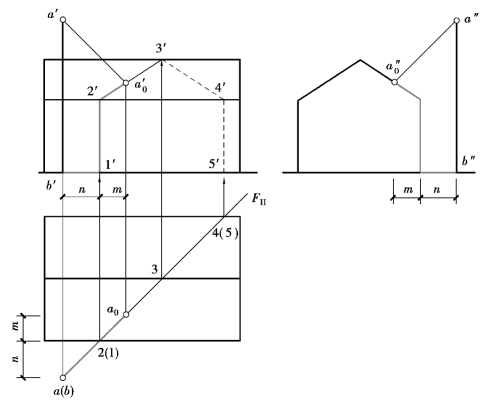
图9.59　铅垂线在房屋上的落影

【例9.17】图9.60（a）为三角形ABC的两面投影图，承影面为V、H，试完成其阴影作图。

【解】作图：如图9.60（b）所示。

①作三角形ABC各顶点的落影AH、BH、CV。

②按原图形各顶点的顺序用直线依次相连得三角形ABC的落影。因C点的影落在V面上，为此再作出C点在H面上的假影（CH），连接AH（CH）、BH（CH）得到折影点Ⅰ0、Ⅱ0，然后再连接并加深AHⅠ0、CVⅠ0、BHⅡ0、CVⅡ0和AHBH。

③判断三角形ABC各投影的阴、阳面，最后着色，完成三角形ABC的阴影作图。

图9.60　平面多边形的落影

2）平面多边形的落影规律

①当平面多边形平行于承影面时，其落影与该多边形的同面投影的大小、形状均相同。

如图9.61所示，水平三角形ⅠⅡⅢ在水平面R上的落影为三角形ⅠRⅡRⅢR。它们的V面投影均积聚成直线，它们的H面投影的大小、形状完全相同，均反映了三角形ⅠⅡⅢ的实形。

图9.61　平面多边形与承影面平行

图9.62　平面多边形与承影面平行时的落影

如图9.62所示，五边形ⅠⅡⅢⅣⅤ平面在铅垂承影面P上的落影为ⅠPⅡPⅢPⅣPⅤP。从H投影中可以看出，五边形的积聚投影12345平行于铅垂承影面P的积聚投影，这说明五边形平面与铅垂承影面P平行。五边形落影的H面投影1P2P3P4P5P重合在承影面P的积聚投影上，落影的V面投影1′P2′P3′P4′P5′P与五边形V面投影1′2′3′4′5′的大小、形状完全相同。

②当平面多边形与光线平行时，该平面多边形在任何承影平面上的落影成一直线，并且平面图形的两面均呈阴面。

图9.63为平面多边形平行于光线方向的3种情况，图（a）是铅垂矩形平面ABCD平行于光线方向，它在H面和V面上的落影是折线AHE0和E0CV。因铅垂矩形平面ABCD只有迎光的边AD和DC被照亮，其他部分均不受光，故两表面为阴面。图（b）是正垂三角形ABC平行于光线方向，它在H上面的落影是一条直线段AHBH。此时，只有迎光的边CA和CB被照亮，其他部分均不受光，故两表面为阴面。图（c）是一般位置的三角形DEF平行于光线方向，它在V和H面上的落影是折线FHⅠ0和Ⅰ0DV。此时，只有迎光的边DF被照亮，其他部分均不受光，故两表面为阴面。

3）平面图形投影的阴、阳面识别

平面图形在光线的照射下，一侧迎光，另一侧必然背光，故有阳面和阴面之分。在投影图中作阴影时，需要判明平面图形的各投影是阳面投影还是阴面投影，以便正确作出直线与平面或平面与平面间的相互落影。

①当平面图形为投影面垂直面时，可在有积聚性的投影中，用光线的同面投影直接识别。

如图9.64（a）所示，正垂面P、Q、R的V面投影有积聚性，只需要判别其H面投影是阳面的投影还是阴面的投影。判别的方法是用光线的V投影s′去照射正垂面P、Q、R在V面上的积聚投影，由于平面P、R与H投影面的倾角小于45°，上表面均为阳面，故其H面投影是阳面投影。而平面Q位于与铅垂方向呈45°的范围内，该范围内的平面对H投影面的倾角大于或等于45°，小于90°，光线照射在Q平面的左下侧面（即阳面），右上侧面为阴面，由上向下作Q平面的H投影时，可见的表面却是Q平面背光的右上侧面，所以Q平面的H的投影是阴面的投影。

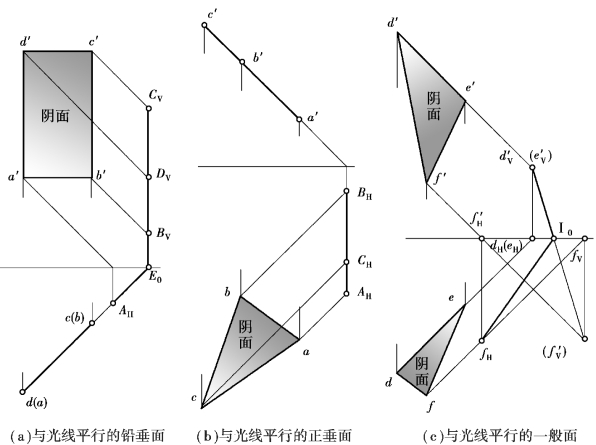
图9.63　与光线平行的多边形平面的落影

图9.64　投影面垂直面的阴、阳面识别

如图9.64（b）所示，铅垂面P、Q、R的H投影有积聚性，由它们的H投影可以判明P、R两平面的V面投影为阳面的投影，Q平面的V面投影为阴面的投影。其识别方法与图9.64（a）完全相同。

②当平面图形处于一般位置时，可先求出平面图形的落影，若平面图形投影的各顶点字母旋转顺序与落影的各顶点字母旋转顺序相同，为阳面投影，相反则为阴面投影。

如图9.65所示，一般位置平面△ABC的落影为AVBVⅡ0CHⅠ0。△ABC的V面投影△a′b′c′与落影AVBVⅡ0CHⅠ0的字母旋转顺序相同，都是顺时针方向，所以△ABC的V面投影△a′b′c′为阳面投影，而H面投影△abc的各顶点字母旋转顺序是逆时针方向，与落影的字母旋转顺序相反，故△ABC的H面投影△acb为阴面的投影。

图9.65　一般位置平面的阴、阳面识别

【例9.18】已知正平面ABCD的两面投影如图9.66（a）所示，试完成其落影作图。

【解】作图：如图9.66（b）所示。

图9.66　正平面的落影

①作正平面的BC边在H投影面上的落影BHCH，该影平行于bc，并且等于bc。

②作铅垂线AB和CD在H投影面上的落影BHⅠ0、CHⅡ0，它们平行于光线S在H面上的投影s，点Ⅰ0、Ⅱ0在OX轴上，是折影点。

③作铅垂线AB、CD在V投影面上的落影AVⅠ0、DVⅡ0，它们分别平行于a′b′、c′d′。连接AVDV得正平线AD在V投影面上的落影。(www.xing528.com)

④将影区涂上暗色，完成落影作图。

4）曲线平面和圆平面的阴影

（1）曲线平面的阴影及基本性质

①曲线平面的阴影作图：首先作出曲线上一系列特征点的落影，即曲线上的连接点、最高点、最低点、最左点、最右点等，如图9.67所示，再用光滑曲线依次连接这些影点，就得曲线平面的落影。然后，由阴阳面的判别方法，确定图形的投影是阴面投影还是阳面投影，并将影区和阴区涂成暗色。

②曲线平面落影的基本性质：当曲线平面平行于承影面，则在该面上的落影与其同面投影的形状、大小相同。

图9.68所示曲线平面为正平面，它在V投影面上的落影与其V投影的形状、大小相同，并反映该曲线平面的实形。

当曲线平面与光线平行时，它在任何承影平面上的落影都成一直线，并且平面图形的两面均呈阴面。

图9.67　曲线平面图形的阴影

图9.68　平行于承影面的曲线平面图形的阴影

（2）圆平面的落影

①当圆平面平行于投影面时，圆在该投影面上的落影与圆本身平行相等，反映圆的实形。作影时，可直接由圆心至承影面的距离按圆半径画影线圆。图9.69（a）是正平圆在V面上的落影作图，图9.69（b）是水平圆在H面上的落影作图。

图9.69　圆在所平行的投影面上的落影

②当圆平面与承影面不平行时，其落影为椭圆。圆心的落影就是落影椭圆的中心，圆的任何一对相互垂直直径的落影成为落影椭圆的一对共轭直径。

图9.70是一水平圆在V面上的落影，其形状为椭圆。为了作出落影椭圆，图中利用了圆的外切正方形各边的中点Ⅰ、Ⅲ、Ⅴ、Ⅶ，以及正方形对角线与圆周的交点Ⅱ、Ⅳ、Ⅵ、Ⅷ等8个点的落影相连而作出。其具体作图步骤如下：

图9.70　水平圆在V面上的落影

a.作圆的外切正方形ABCD，边AD、BC为正垂线，AB、CD为侧垂线。圆周切于正方形四边的中点Ⅰ、Ⅲ、Ⅴ、Ⅶ，与对角线AC、BD的四个交点为Ⅱ、Ⅳ、Ⅵ、Ⅷ。

b.按直线落影规侓及方法作出外切正方形ABCD在V面上的落影AVBVCVDV，其形状为平行四边形。影线AVDV、BVCV是45°线，AVBV、CVDV平行于投影轴OX，其长度等于圆的直径2R；对角线BVDV是铅垂线；对角线BVDV和AVCV的交点OV是圆心O的落影。过点OV作OX轴的平行线和45°线分别交落影四边形各边于中点ⅠV、ⅢV、ⅤV、ⅦV，它们是落影椭圆上的点，也是正方形各边与圆周相切之点Ⅰ、Ⅲ、Ⅴ、Ⅶ的落影。

c.圆与正方形对角线交点Ⅱ、Ⅳ、Ⅵ、Ⅷ的落影，是由点E、F之影EV、FV作圆平面积聚投影的平行线与正方形落影的对角线相交而求得的。而影点EV、FV是根据在平行光线照射下，点分线段成定比，其落影后比值不变这一原理作出的。在H投影中，等腰直角三角形△o7b与△oe6相似，。在V投影中，△OVBVⅦV也是等腰直角三角形，。由以上两等式便可得出OVEV=R。用同样的方法可求得OVFV=R。因此，影点ⅠV、DV、FV、ⅤV、BV、EV六点共圆，该圆的半径等于已知圆平面的半径R。

d.用光滑的曲线依次连接影点ⅠV、ⅡV、ⅢV、ⅣV、ⅤV、ⅥV、ⅦV、ⅧV等8个点，即得水平圆在V面上的落影椭圆。

③水平半圆在墙面上的落影。

在房屋建筑上常有紧靠墙面的半圆形物体，如半圆形的雨篷板、挑出墙面的半圆柱形阳台及其他装饰物等，所以需要作嵌在墙面上的水平半圆的落影。

如图9.71（a）所示，将半圆周四等分，定出圆周上的Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ点的V、H投影。Ⅰ、Ⅴ点的落影ⅠV、ⅤV与自身重合；Ⅱ点的影ⅡV在3′的正下方，即中心线上；Ⅲ点的影ⅢV在5′的正下方；Ⅳ点的影ⅣV到圆中心线的距离是4′到圆心距离的2倍。将这5个特殊方位的点的落影ⅠV、ⅡV、ⅢV、ⅣV、ⅤV连接成所求的影。

图9.71（b）是用点落影的单面作图的方法画水平半圆的落影。半圆周上各点到V投影面的距离可在图中作半圆求出，然后按点落影的单面作图求出半圆周上各点的落影，再连接它们成所求的影。

图9.71（c）是采用水平圆在V投影面上落影的八点共圆法作出的。

图9.71　圆平面不平行于承影面时的落影作图

【例9.19】已知水平圆O的V投影，圆心距V投影面为50，用单面作图完成水平圆O的V面落影。

【解】作图：①用点落影的单面作图方法求圆心O的落影OV。自OV作水平中心线和铅垂中心线，如图9.72（a）所示。

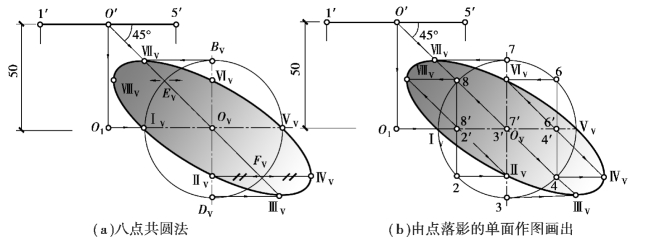
图9.72　水平圆的V面落影单面作图

②以OV为圆心、o′1′为半径画圆，与过OV的水平中心线交于ⅠV、ⅤV，与过OV的铅垂中心线交于BV、DV，与过OV的光线s′交于EV、FV。

③自BV、DV分别作已知圆积聚投影的平行线与过OV的光线s′相交于影点ⅦV、ⅢV。

④由EV、FV分别作已知圆积聚投影的平行线与过OV的铅垂中心线相交于影点ⅡV、ⅥV。

⑤利用椭圆上的点对长短轴对称的特性，作出影点ⅡV、ⅥV的对称影点ⅣV、ⅧV。

⑥用曲线依次光滑连接影点ⅠV、ⅡV、ⅢV、ⅣV、ⅤV、ⅥV、ⅦV、ⅧV成椭圆。

以上步骤是八点共圆法画落影椭圆的单面作图。该题还可用点落影的单面作图来完成，如图9.72（b）所示。其作图步骤也是先由已知圆心距V投影面的距离作出圆心O的落影OV，再以OV为圆心作一个与已知圆相等的圆，然后按点落影的单面作图方法画出前半圆的影。后半圆影的画法与前半圆相似，只是各条作图线的方向相反。如自水平直径ⅠVⅤV上的点6′向上作铅垂线交圆周于点6，由点6向左作水平线与过点6′的光线V投影s′的反向相交于影点ⅥV，其余各点的影作法相同。也可以用这一方法作正平面圆的H面落影和侧平面圆的V面落影。