1)直线段的落影概念
直线段的落影是射于该直线段上各点的光线所形成的光平面与承影面的交线,如图9.8所示。
2)直线段的落影作图
(1)直线段在一个平面上的落影作图
直线段在一个平面上的落影作图通常是求直线段两端点同面落影的连线。如图9.49所示,直线段AB的两端点距V面的距离小于距H面的距离,所以直线段AB的两端点的影都落在V面上,则直线段AB的影也在V面上。其作图步骤是:首先过直线段的两端点A、B分别引光线S(s,s′),自点a、b的光线H投影s先与OX轴相交于点aV、bV,再由点aV、bV分别作铅垂线与过点a′、b′的光线V投影s′相交于点a′V、b′V,用直线段连接a′Vb′V便得到直线段AB在V面上的落影AVBV。
(2)直线段在两相交平面上的落影作图
直线段的影落在两相交平面上,其影为折线,折影点在两平面的交线上。如图9.50所示,直线段CD的端点C距H面的距离小于距V面的距离,其影在H面上,而端点D距V面的距离小于距H面的距离,其影在V面上。连线时应遵循线段两端点在同一平面上的影才能相连的原则,为此,利用假影找出该线段落在OX轴上的折影点,从而作出直线段CD在V、H面上的落影。为求直线段CD的落影,首先过直线段的两端点C、D分别引光线S(s,s′),自点c′的光线V投影s′先与OX轴相交于点c′H,由点c′H作铅垂线与过点c的光线H投影s相交于影点cH,这是端点C在H面上的真影CH。而端点D的影是自点d的光线H投影s先与OX轴相交于点dV,由点dV作铅垂线与过点d′的光线V投影s′相交于影点d′V,这是端点D面在V面上的真影DV。由于直线段CD的两端点的影不在同一个平面上,不能连线,故再作端点C或端点D的假影。图中作的是端点D在H面上的假影DH(dH,d′H)。连接cHdH与OX轴相交于折影点E(e,e′),再连接e′d′V,即完成直线段CD在两相交平面V、H上的落影作图。
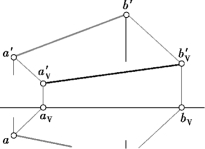
图9.49 直线在一个平面上的落影作图
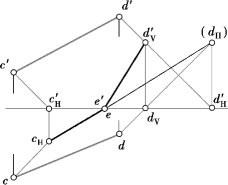
图9.50 直线在两个平面上的落影作图
3)直线段的落影规律
在正投影图阴影中的直线段落影规律与轴测图阴影中的直线段落影规律相似,只是在图中的表现形式不同。
(1)平行规律
①若直线段平行于承影面,则落影与该线段的同面投影平行且等长。
图9.51中,因直线AB的H投影ab∥PH,故直线AB平行于铅垂面P,它在P平面上的落影APBP∥AB,APBP=AB。反映在投影图中是:a′b′∥b′Pb′P,a′b′=b′Pb′P,ab∥aPbP,ab=aPbP。在作影过程中,只需求出直线段的一个端点的落影,便可按平行、等长的关系画出该直线段的落影。
②一直线在诸平行承影面上的落影彼此平行。
图9.52中的承影面P平行于承影面Q,含直线AB的光平面与两个平行平面相交的两条交线必然相互平行,也就是直线AB在P、Q两个承影面上的落影相互平行,即APCP∥CQBQ。这两段落影的同面投影也相互平行,即b′Pc′P∥c′Qb′Q,aPcP∥cQbQ。在投影图中可先求出A、B两端点的落影AP(aP,b′P)和BQ(bQ,b′Q),它们位于两个承影面上,不能连线。为此,在H投影中,由承影面P右边线的积聚投影(也是直线AB上的点C在P平面右边线上落影的H投影cP)作光线H投影的反方向交ab于点c,自点c作铅垂线交a′b′于点c′,再过点c′作光线的V投影交P平面右边线的V投影于点c′P,连接b′Pc′P得直线AB在P平面上落影的V投影。又由b′Q作b′Pc′P的平行线便可完成直线AB的落影作图。直线AB上的C点在P平面右边线上的影点CP称为滑影点。
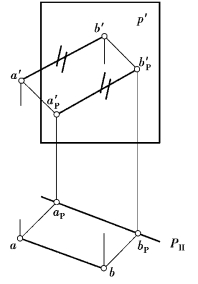
图9.51 直线在其平行面上的影

图9.52 直线在二平行承影面上的落影
③诸平行直线在同一承影面上的落影彼此平行。
如图9.53所示,直线AB∥CD,则含直线AB和CD的光平面相互平行,它们与承影面P的交线必然相互平行,也就是两直线的落影相互平行,即APBP∥CPDP。它们的同面投影也相互平行,即a′Pb′P∥c′Pd′P,aPbP∥cPdP。
④诸平行直线在诸平行承影面上的落影彼此平行。
该规律是规律②、③的推论。
⑤直线平行于光线,其落影为一点。
如图9.54所示,直线段AB∥光线S,则通过AB的光线只有一条,它与承影面也只有一个交点,所以直线段AB的落影为一点。在投影图中表现为ab的方向与光线的H面投影s方向相同,a′b′的方向与光线的V投影s′的方向相同,都是45°线。
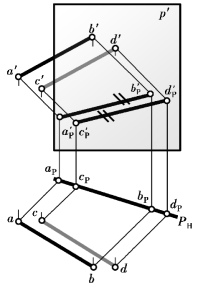
图9.53 二平行线在一平面上的影(https://www.xing528.com)
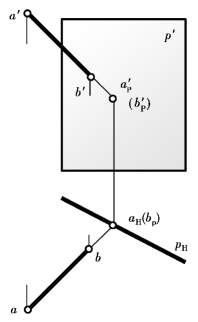
图9.54 直线平行于光线的影
(2)相交规律
①若直线与承影面相交,直线的落影必通过该直线与承影面的交点。
在图9.55中,直线段AB延长后与承影面P相交于点K。交点K属于承影面P,故其落影KP为K点本身;又因影点KP应在直线AB落影的延长线上,所以直线AB的影必然通过交点K。作图时,只需作出直线的一个端点的落影,如A点的落影AP(aP,a′P),连接a′Pk′,再由b′作光线的V投影s′交a′Pk′于点b′P,影线a′Pb′P为直线段AB在承影面P上落影的V投影。
②相交两直线在同一平面上的落影必相交,且交点的落影为两直线落影的交点。
如图9.56所示,直线AB与BC交于点B,作图时首先求出交点B的落影BP(bP,b′P),再分别求出每一直线的任一端点的影,如AP(aP,a′P)和CP(cP,c′P),即可确定两相交直线的落影。
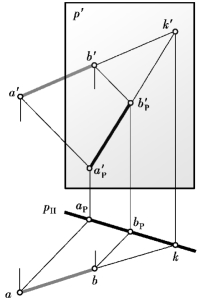
图9.55 直线与承面相交
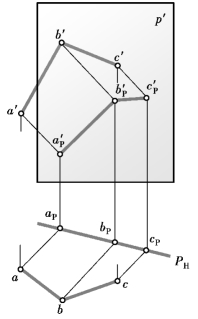
图9.56 相交两直线的影
③一直线在两相交平面上的落影为一折线,折影点在两平面的交线上。
如图9.57所示,铅垂承影面P和Q的交线为DE,直线段AB在P、Q两相交承影面上的落影,是过直线AB的光平面与二承影面的交线。作为影线的两条交线必然交于一点C0(即三面共点),而点C0自然在交线DE上,这就是折影点。首先分别作出直线两端点A、B在承影面P、Q上的落影AP(aP,a′P)和BQ(bQ,b′Q),它们是不同承影面上的两个影点,不能连线,为此,必须求出折影点C0。求折影点的方法是利用直线上任意两点同面落影连线。由于两点取在直线的不同位置,则有以下作图方法之分——回投光线法、延棱扩面法、端点虚影法、辅助点法等。
a.回投光线法:如图9.57所示,铅垂承影面P和Q的交线DE为一铅垂线。因折影点C0属于铅垂线DE,故折影点C0的H投影c0重影于积聚投影d(e)。由c0作光线H投影s的反方向交ab于点c,自点c作铅垂线交a′b′于点c′,再过点c′作光线的V投影s′交d′e′于点c′0,这就是折影点的V投影。连线a′Pc′0、c′0b′Q,就是所求影线的V投影。
b.延棱扩面法:如图9.57所示,扩展承影面Q,求出直线AB与Q平面的交点K(k,k′)。影线BQK与两承影面的交线DE相交于折影点C0。
c.端点虚影法:如图9.57所示,求出端点B在P平面的扩大面上的假影BP(bP,b′P),连线a′Pb′P与P、Q二平面的交线d′e′的交点c′0,即是折影点C的V投影。
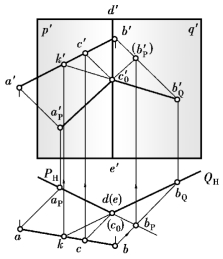
图9.57 一直线在相交平面上的影
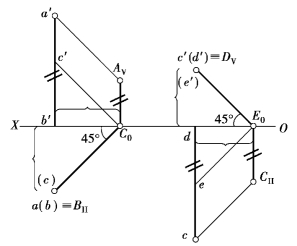
图9.58 投影面垂直线在投影面上的落影
(3)垂直规律
①投影面垂直线在所垂直的投影面上的影为45°线,而在另一投影面上的影与自身平行,其距离等于直线到承影面的距离。
如图9.58左图所示,AB为铅垂线,含直线AB的光平面为铅垂面,它与承影面H的交线BHC0和OX轴成45°,此交线也是该光平面的积聚投影;含直线AB的光平面与承影面V的交线AVC0垂直于OX轴,平行于直线AB。在投影图上,影线AVC0平行于a′b′,影线AVC0到a′b′的距离等于AB到V面的距离。
在图9.58右图中,直线CD为正垂线,包含CD的光平面为正垂面,它与承影面V的交线DVE0和OX轴成45°,此交线也是该光平面的积聚投影;含直线CD的光平面与承影面H的交线CHE0垂直于OX轴,平行于直线CD。在投影图上,影线CHE0平行于cd,影线CHE0到cd的距离等于CD到H面的距离。
②投影面垂直线在物体表面上的影的投影为:
a.在该直线所垂直的投影面上的影的投影为45°线。
b.影的其余两个投影呈对称图形。
铅垂线AB在房屋上的落影如图9.59所示。因含AB的铅垂光平面与房屋阳面的交线为其影线,影线的H投影与光平面的积聚投影重合,为45°直线,说明含AB的铅垂光平面与投影面V、W的夹角均为45°,所以含AB的铅垂光平面与房屋交线的V、W投影呈对称图形,作影时可直接用对称关系作图。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




