画法几何与阴影透视技法

当直线和曲面体的投影都没有积聚性时，只能应用作辅助面的方法来解决。其解题步骤与求直线与平面立体的交点相类似，即：

①包含已知直线作一辅助截平面。

②求出截平面与已知曲面体的截交线。

③求出截交线与直线的交点，即为所求直线与曲面体的交点（贯穿点）。

解题的关键是如何根据曲面体的性质来选取适当的辅助截平面，使它和已知曲面体的截交线的投影是简单易画的图形。

【例7.11】求直线AB与圆锥的贯穿点。

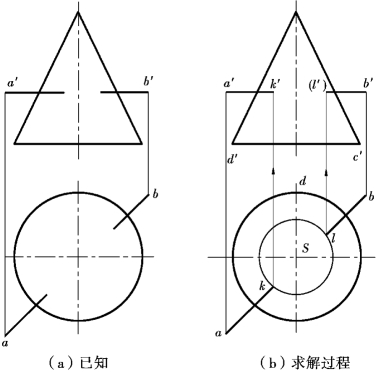
图7.19　水平直线与圆锥相交

【解】分析：由于直线AB是水平线，故可包含直线AB作水平辅助截平面P。P平面与圆锥的截交线为水平圆，其H投影反映实形，它与直线AB的H投影ab的交点k、l即为所求交点的H投影。再对应求出V投影k′、l′。

投影作图：如图7.19（b）所示。

可见性判断：圆锥的H投影为可见，故交点的H投影为可见；在V投影中k′可见，l′为不可见。

【例7.12】如图7.20所示，求直线AB与斜圆柱的贯穿点。

【解】分析：包含直线AB作平行于斜圆柱轴线的平面为辅助截平面，其截交线为平行四边形，故可通过B点作一直线BN平行于斜圆柱轴线。由AB和BN所决定的辅助截平面，截斜圆柱所得的截交线为平行四边形ⅠⅡⅢⅣ，如图7.20（a）所示。

投影作图：如图7.20（b）所示。

①作直线BN平行于斜圆柱轴线，并求出BN与斜圆柱底面所在平面的交点N。

②求出直线AB与斜圆柱底面所在平面的交点M。连接MN交斜圆柱底圆于Ⅰ、Ⅱ；过Ⅰ、Ⅱ作斜圆柱的素线ⅠⅣ和ⅡⅢ，则平行四边形ⅠⅡⅢⅣ为辅助截平面与斜圆柱的截交线。

③AB与截交线ⅠⅡⅢⅣ的交点K、L即为所求的贯穿点。

④判别可见性：直线AB从前半斜圆柱面穿过，由其投影确定k′、l′和k、l均为可见。

【例7.13】如图7.21所示，求一般线AB与圆锥的贯穿点。(www.xing528.com)

【解】分析：如果包含直线AB作辅助正垂面或铅垂面，则截割圆锥所得截交线是椭圆或双曲线，作图较困难。但从图7.12中可知，截平面通过锥顶时，截交线为一三角形。因此，可以由锥顶和直线AB所决定的平面作为辅助面。

投影作图：如图7.21（b）所示。

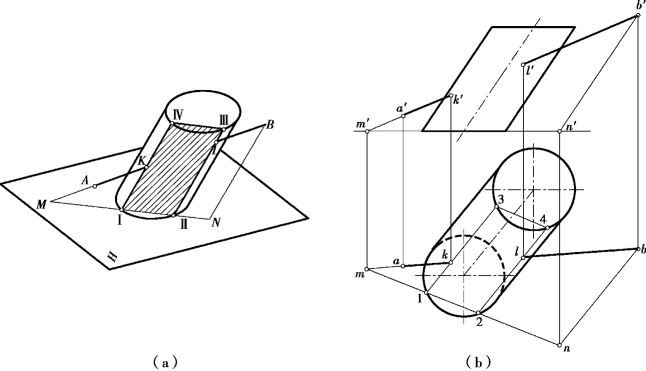
图7.20　直线与斜圆柱的贯穿点

①求锥顶S和直线AB所确定的辅助平面与圆锥的截交线。为此，连接SA，并延长使其与圆锥底面所在平面相交，其交点为E；再取直线AB的任一点C，连接SC，并延长使它与圆锥底面所在平面相交，其交点为F；连接EF交圆锥底圆于Ⅰ、Ⅱ；又连接SⅠ、SⅡ，则△SⅠⅡ为辅助平面与圆锥的截交线。

②截交线与直线AB的交点M、N即为所求贯穿点。

③判别直线AB的可见性：直线AB从前半圆锥表面穿过，故其投影均为可见。

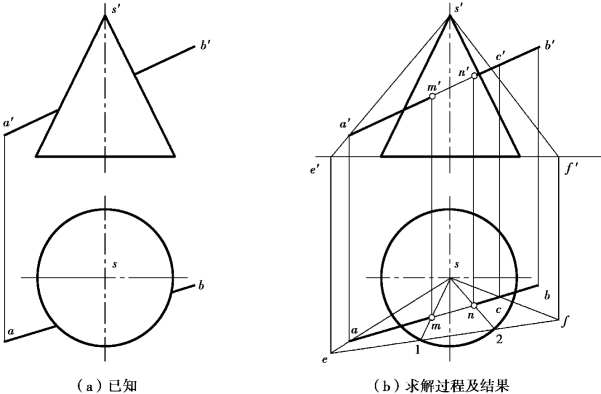
图7.21　一般线与圆锥相交

【例7.14】如图7.22（a）所示，作直线EF与圆球的贯穿点。

【解】分析：直线EF为一般位置直线，如果包含该直线作投影面垂直面为辅助平面，则辅助平面与圆球的截交线圆的另外两投影为椭圆，作图比较麻烦，准确性又较差。于是，用一次换面法作出截交线圆的实形和直线EF的实长投影e1′f1′，它们的交点k1′、l1′即为所求贯穿点K、L的新投影。最后将其返回到K、L点的各个原投影上。

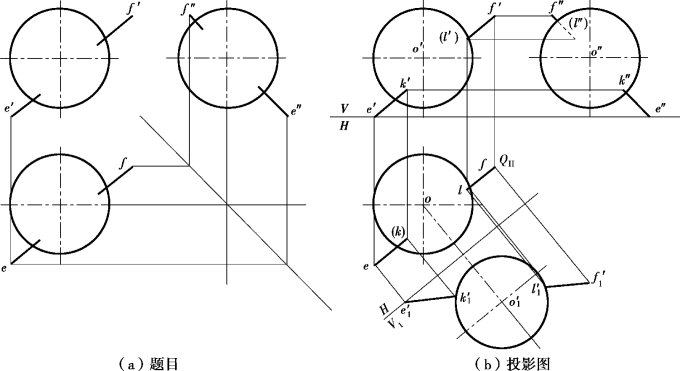
图7.22　直线与圆球的贯穿点

投影作图：如图7.22（b）所示。

①过EF直线作铅垂面Q，显然QH与ef重合。

②取新投影面V1∥Q，用换面法在V1面上作出截交线圆的实形和直线EF的实长投影e1′f1′，直线e1′f1′与圆o1′的交点k1′、l1′即为贯穿点的新投影。

③将属于e1′f1′的点k1′l1′反投影到ef，即得所求贯穿点的水平投影k、l。根据直线的点的投影对应关系，求出贯穿点K、L的正面投影和侧面投影。

④判别可见性：直线EF由前、下、左半球穿入球体，从后、上、右半球穿出球体。