【摘要】:当曲面垂直于某一投影面或直线垂直于某一投影面时,可利用积聚性用曲面上取点的方法求出交点。如图7.17所示,求直线AB与正圆柱体的贯穿点。又由于正圆柱面的水平投影有积聚性,所以当直线AB与圆柱面相交时,交点的水平投影必属于圆柱面的积聚投影。②在水平投影中,ab与圆周的交点n为另一贯穿点N的水平投影,由n向上引垂线与a′b′交于点n′,则点n′即为贯穿点N的正面投影。图7.18直线与圆锥相交
当曲面垂直于某一投影面或直线垂直于某一投影面时,可利用积聚性用曲面上取点的方法求出交点。
【例7.9】如图7.17(a)所示,求直线AB与正圆柱体的贯穿点。
【解】分析:因圆柱顶面的正面投影和侧面投影都有积聚性。当直线AB与圆柱顶面相交时,交点的正面投影和侧面投影必属于圆柱顶面的积聚投影。又由于正圆柱面的水平投影有积聚性,所以当直线AB与圆柱面相交时,交点的水平投影必属于圆柱面的积聚投影。
投影作图:如图7.17(b)所示。
①在正面投影中,直线a′b′与圆柱顶面的正面投影的交点m′,即为贯穿点M的正面投影。由m′向下引垂线与ab的假想连接线交于m,则m为贯穿点的水平投影。
②在水平投影中,ab与圆周的交点n为另一贯穿点N的水平投影,由n向上引垂线与a′b′交于点n′,则点n′即为贯穿点N的正面投影。
③判别可见性:如图7.17(c)所示,在正面投影中,因贯穿点N属于前半圆柱面,其正面投影n′为可见,故自点n′到圆柱轮廓素线的那一段线为可见。贯穿点M属于顶面,故在水平投影中mb为可见。
【例7.10】如图7.18(a)所示,求直线CD和圆锥的贯穿点。(https://www.xing528.com)
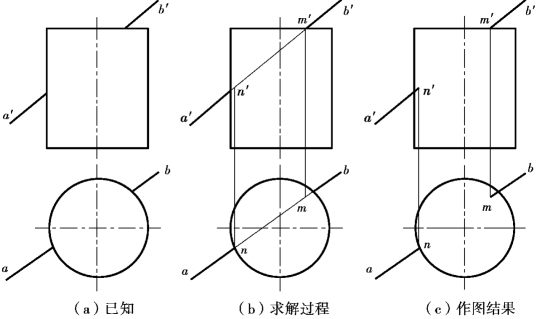
图7.17 直线与圆柱相交求贯穿点
【解】分析:由于直线CD垂直于H面,所以交点的H投影m、n与直线CD的积聚投影cd重合。故在H投影中经过积聚投影,即过m点在锥面上作一条素线s1,便可求出s′1′;再由m点向上作铅垂联系线与s′1′交于m′,由m1、m′定出m″。
投影作图:如图7.18(b)所示。
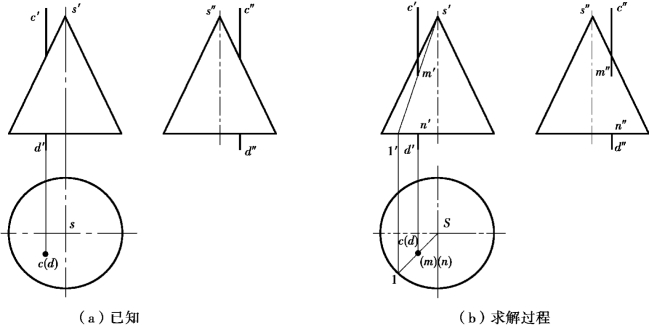
图7.18 直线与圆锥相交
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




