画法几何与阴影透视：非回转直线曲面教程

1）柱面

（1）柱面的形成

直母线ⅠⅡ沿着一曲导线L移动，并始终平行于一直导线AB而形成的曲面称为柱面。曲导线L可以是闭合的或不闭合的，如图6.9（a）所示。此处曲导线L是平行于H面的圆，AB是一般位置直线。由于柱面上相邻两素线是平行二直线，能组成一个平面，因此柱面是一种可展曲面。

（2）柱面的投影

①画出直导线AB和曲导线L（圆L∥H）的V、H投影（即a′b′、ab，l′、l）。

②画轴OO1的V、H投影。显然，轴OO1∥AB，且O1点属于H面，故作o′o′1∥a′b′，oo1∥ab。

③画出母线端点Ⅱ运动轨迹L1的V、H投影。显然，L1线属于H面。画L1线的H投影：以o1为圆心，以圆L的半径为半径画圆即得。L1线的V投影积聚成一段直线，在OX轴上，长度等于直径。

④画出柱面的V面投影轮廓线，即画出柱面上最左素线ⅠⅡ和最右素线ⅢⅣ的V面投影，如图6.9（b）中的1′2′、3′4′。ⅠⅡ、ⅢⅣ不是柱面H投影的轮廓线，其H投影12、34不必画出。

⑤画出柱面的H投影轮廓线，即在H面中作l、l1两圆的公切线56、78即得。它们的正面投影5′6′、7′8′不必画出。

需要注意的是，若曲导线L不封闭（上述曲导线L是圆，故是封闭的），则要画出起、止素线的V、H投影。虽然直导线AB的位置和曲导线L的形状、大小可根据实际需要来确定，但其投影的画法仍如上述。

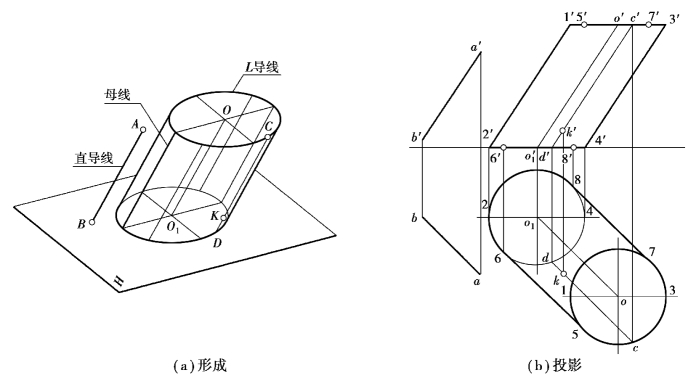
图6.9　柱面的形成和投影

（3）柱面投影的可见性

①V投影。V投影是前半柱面和后半柱面投影的重合，最左（ⅠⅡ）素线、最右（ⅢⅣ）素线是前后半柱面的分界线，也是可见与不可见的分界线，故包含曲线Ⅰ、Ⅴ、Ⅲ（H投影中逆时针顺序）的部分是可见的，包含曲线Ⅲ、Ⅶ、Ⅰ（H投影中逆时针顺序）的部分是不可见的。

②H投影。素线ⅤⅥ和ⅦⅧ的H投影是柱面的H投影轮廓线，也是可见与不可见的分界线，包含曲线ⅤⅠⅦ的部分是可见的，包含曲线ⅤⅢⅦ的部分是不可见的。

（4）取属于柱面的点

①已知：属于柱面的一点K的V投影k′（k′是可见点），求作其H投影k。

②方法：用素线法，即过点K作一属于柱面的素线CD，点C属于圆L，点D属于L1圆。作出CD的V、H投影cd，则K点的H投影k必属于cd。

③作图：过k′作c′d′∥a′b′（或者1′2′），点c′属于l′，点d′属于l′1；由c′向下引垂线交l的前半圆于c点，由d′引垂线交l1的前半圆于d点，连接cd；再由k′向下引垂线交cd得k。因K点所属柱面的H投影为不可见，故k为不可见。

（5）柱面的应用举例

柱面的应用实例为菲律宾国际机场，如图6.10所示。

(www.xing528.com)

图6.10　菲律宾国际机场

2）锥面

（1）锥面的形成

一直母线SI沿着一曲导线L移动，并始终通过一定点S而形成的曲面称为锥面。S为锥顶点。曲导线L可以是闭合的或不闭合的。如图6.11（a）所示，导线L是H面上的一个圆线。由于锥面相邻两素线是相交二直线，能组成一个平面，因此锥面是可展曲面。

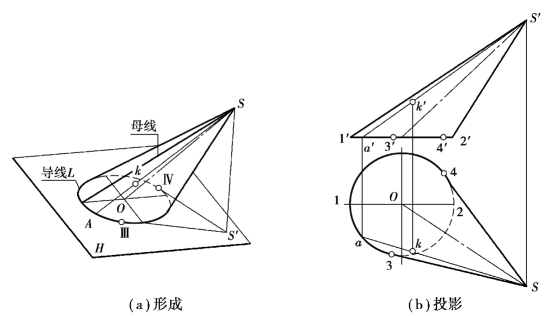
图6.11　圆锥面的形成和投影

（2）锥面的投影

①画出导线L和顶点S的V、H投影l′、l和s′、s，并用点画线连接s′、o′、so。

②画锥面的V投影，即最左素线SⅠ和最右素线SⅡ的V投影s′1′和s′2′。

③画锥面的H投影，即过s向圆l作的两条切线s3和s4。

同理，若导线L不封闭，则要画出起、止素线的V、H投影。

（3）锥面投影的可见性

①如图6.11（b）所示，V投影是锥面前半个锥面和后半个锥面投影的重合，最左和最右素线是前、后部分的分界线。也是可见与不可见的分界线。由H投影知，锥面S-Ⅰ、Ⅲ、Ⅱ部分可见，锥面S-Ⅰ、Ⅳ、Ⅱ部分不可见。

②由V投影知，锥面S-Ⅲ、Ⅰ、Ⅳ部分可见，锥面S-Ⅲ、Ⅱ、Ⅳ部分不可见。

（4）取属于锥面的点

①已知：属于锥面的一点K的H投影k，求其V投影k′。

②作图：采用素线法，连接sk与圆l相交于a；由a向上作垂线与l′相交于a′，并连接s′a′；由k向上作垂线与s′a′相交于k′，即为所求。

（5）锥面应用举例

锥面的应用实例为美国古根海姆博物馆，如图6.12所示。

图6.12　美国古根海姆博物馆