在画法几何中,通常是根据曲线的投影来研究曲线的性质及其画法的。因为曲线可看作由点的运动而形成,只要作出曲线上一系列点的投影,并将各点的同面投影依次光滑地连接起来,即得到该曲线的投影。
(1)曲线投影的性质
曲线的投影一般仍为曲线,在特殊情况下,当平面曲线所在的平面垂直于某投影面时,它在该投影面上的投影为直线。
曲线的切线在某投影面上的投影仍与曲线在该投影面上的投影相切;二次曲线的投影一般仍为二次曲线,如圆和椭圆的投影一般为椭圆。
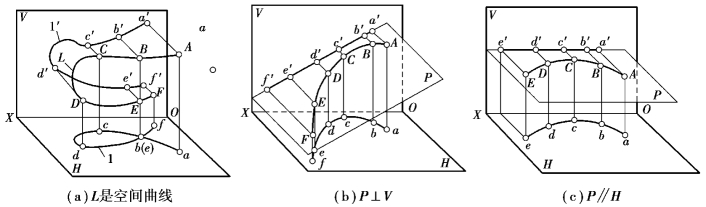
图6.2 曲线的投影
(2)圆的投影
圆是平面曲线,当它所在的平面平行于投影面时,其投影反映实形;当圆所在的平面垂直于投影面时,其投影积聚成一直线段,且该线段的长等于圆直径;若圆所在的平面倾斜于投影面,其投影为一椭圆。
【例6.1】如图6.3所示,已知圆L所在平面P⊥V面,P与H面的倾角为α,圆心为O,直径为φ,求圆L的V、H投影。
【解】分析:①由于圆L所在平面P⊥V面,其V投影积聚为一直线l′,l′=直径φ,l′与OX轴的夹角=α。(https://www.xing528.com)
②圆L所属平面倾斜于H面,其H投影为一椭圆l,圆心O的H投影是椭圆中心O,椭圆长轴是圆L内平行于H面的直径AB的H投影ab,ab=AB(直径),椭圆短轴是圆L内对H面最大斜度方向的直径CD的H投影cd,cd=CD·cosα。CD∥V,故c′d′=φ。
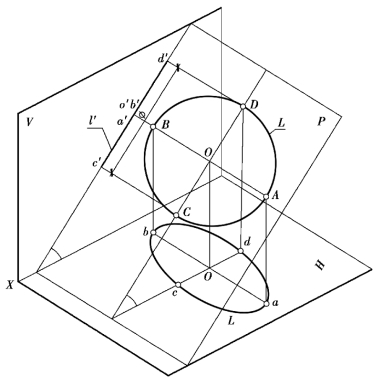
图6.3 垂直于V面的圆的投影
作图:①确定OX轴及圆心O的V、H投影o′,o,如图6.4(a)所示。
②作圆L的V投影l′,即过o′作c′d′与OX轴的夹角=α,取o′d′=φ/2,如图6.4(a)所示。
③作圆L的H投影椭圆l,先作椭圆的长短轴。即过O作长轴ab⊥ox,ao=ob=φ/2,过o作短轴cd∥OX,cd的长度由c′d′确定,如图6.4(b)所示。
④由长短轴可作出椭圆。这里采用换面法完成椭圆作图。如图6.4(c)所示,作一新投影面H1∥圆L,则圆L在H1上的投影l1反映实形。在投影图中作新投影轴O1X1∥l′。根据o、o′作出o1,并以o1为圆心、φ为直径作圆,就得到圆l1=圆L。由圆的l1和l′而得椭圆l。为此,需定出椭圆的足够数量的点,然后用曲线板依次光滑地连接起来。图中示出了e、f点的作图。先在l1上定e1、f1,向O1X1作垂线,与l′交得e′、f′,再过e′、f′向OX轴作垂线,并在此垂线上量取e、f点分别到OX轴的距离等于e1、f1点分别到O1X1轴的距离而定出e、f点。
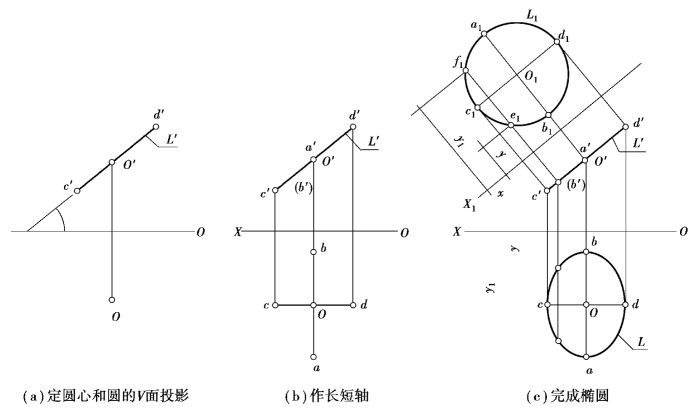
图6.4 作垂直于V面的圆的投影
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




