【例4.11】如图4.23(a)所示,求直线AB的实长和倾角α。
【解】分析:欲求水平倾角,旋转时应保持水平倾角不变,应选择垂直于H面的旋转轴。令旋转轴过A点,在旋转过程中A点将不动,只需将B点旋转。
作图:如图4.23(b)所示。
①在水平投影图中,以a为圆心、ab为半径作bb1圆弧,使ab1∥x。
②在正投影图中,由点的旋转规律知,B点正投影应做平行于投影轴的直线移动,即由b′→b′1,b′b′1∥x,得b′1。
③连接a′b′1即获得反映AB直线实长的投影;a′b′1与X轴的夹角即为所求倾角α。
图4.23(b)中旋转轴的位置很明显,在应用时旋转轴经常无须指明,而图4.23(c)则表示了一般位置直线AB绕不指明位置的铅垂轴旋转成正平线的情况。由于保证了旋转时其水平投影长度不变,正面投影高差不变,故旋转后的正投影反映该直线实长和倾角。由此可见,若旋转轴性质不变,仅改变其位置,对旋转后的结果是没有影响的。在解题中,为了使图面更加清晰,常采用不指明轴的旋转法。
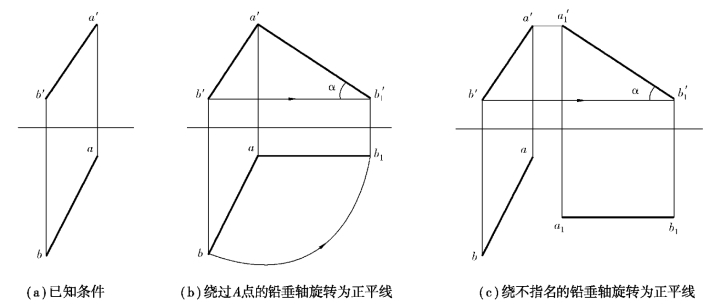
图4.23 求直线的实长及倾角α
【例4.12】如图4.24(a)所示,求平面△ABC的倾角α。
【解】分析:由于需要求出平面的水平倾角α,所以必须绕铅垂轴旋转;若要将一般位置面旋转成正垂面,则必须将属于△ABC的一条水平线旋转为正垂线。
作图:用绕不指明轴旋转法,如图4.24(b)所示。
①在△ABC中作水平线AD,由a′d′∥X,a′d′→ad。
②将AD绕铅垂轴旋转成正垂线的同时(即a1d1⊥X),用△abc≌△a1b1c1求出△ABC新的水平投影△a1b1c1。
③过a′、b′、c′分别作平行于X轴的直线,并以a′1a1⊥X、b′1b1⊥X、c′1c1⊥X,求出a′1b′1c′1,此投影具有积聚性。
④积聚投影a′1b′1c′1与X轴的夹角即为所求α。
用同样的思考方法,可求出平面的正面倾角β。如图4.25所示,在△ABC上作正平线BE,将正平线BE绕正垂轴旋转成铅垂线。根据平面绕垂直轴旋转的投影规律,有△a′b′c′≌△a′1b′1c′1。过a、b、c分别作平行于X的直线,由a1a′1⊥X、b1b′1⊥X、c1c′1⊥X,得到△ABC具有积聚性的投影a1b1c1,它与X轴的夹角即为△ABC的β。
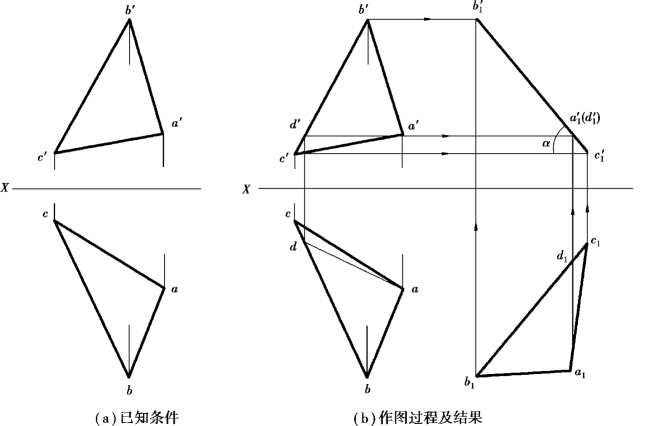
图4.24 求△ABC的倾角α
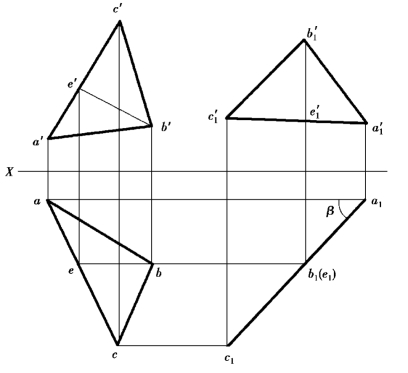
图4.25 求△ABC的倾角β
【例4.13】如图4.26(a)所示,过点C作直线CD与AB垂直相交,求CD。
【解】分析:当直线AB垂直于某一投影面时,由于AB⊥CD,直线CD一定平行于该投影面,且反映实长。同时,在该投影面上的投影反映出AB⊥CD的直角。因此,需将直线AB旋转成垂直线;而一次旋转只能将一般位置直线旋转成平行线(如例4.11),还需将平行线再次旋转成垂直线,所以本例应进行二次旋转。(https://www.xing528.com)
作图:用不指明垂直轴旋转法,如图4.26(b)所示。
①第一次旋转,使AB直线成为正平线A1B1,C点按“三同”原则随着直线AB一起旋转至C1,即a1b1∥X,a1b1=ab;c1与a1b1的相对位置与旋转前c与ab的相对位置保持不变,以点、直线绕垂直轴旋转的规律,作出a′1b′1及c′1。
②第二次旋转,使A1B1直线变换成铅垂线A2B2,C1点按“三同”原则随A1B1一起旋转,即a′1b′1=a′2b′2,a′2b′2⊥X。c′2与a′2b′2的相对位置与旋转前c′1与a′1b′1的相对位置保持不变,c′2c2⊥X,同样以点、直线绕垂直轴旋转的规律,作出a2、b2及c2。
③过点C作直线CD垂直于AB。由于此时a2b2已积聚,它与c2的连线c2d2就是反映垂线CD实长的投影,其正投影平行于X轴(c′2d′2∥X)。
④按旋转前后旋转轴所垂直投影面中的投影,其相对位置不变的规律,且由D点是属于AB直线上的,逐次返回,求出D点的各个投影d1、d′1、d、d′,与C点同名投影的连线就是距离的各个投影。
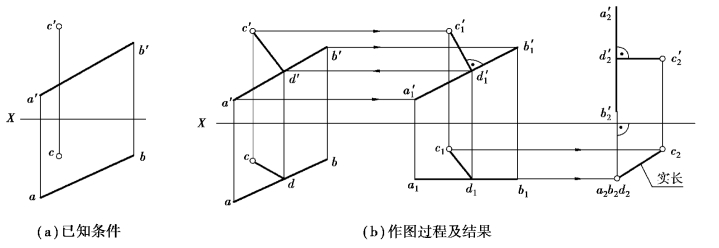
图4.26 求C点到直线AB的距离
【例4.14】如图4.27(a)所示,求一般位置平面△ABC的实形。
【解】分析:为求△ABC的实形,需将△ABC旋转成平行平面。在两面体系中,平行面的倾角一个为90°,一个为0°。从例4.12中可获得启示:先用一次旋转将△ABC旋转成垂直面,产生一个具有90°倾角的积聚投影,保持这个90°倾角不变(在投影图中体现为积聚投影不变),再进行一次旋转,产生另一个倾角为0°的投影,该投影反映△ABC的实形。
作图:如图4.27(b)所示,综合运用不指明垂直轴和指明垂直轴旋转法。
①第一次旋转,绕过不指明的正垂轴,将△ABC旋转成铅垂面。其作图方法同例4.12,产生c′1a′1b′1、c′1a′1b′1具有积聚性的正面投影a1b1c1及△a′1b′1c′1。
②第二次旋转,绕过C点的铅垂轴旋转,将积聚投影a1b1c1旋转至平行于X轴的位置,即a2b2c2∥X。由平面绕垂直轴旋转的规律,作出△a′2b′2c′2,即为△ABC的实形。
【例4.15】如图4.28(a)所示,求直线AE与平面△ABC的夹角θ。
【解】分析:可以把平面△ABC通过两次旋转,使它变换成平行面。此时,直线AD(其中A点是直线与平面的共有点)也随着平面进行旋转。在平面△ABC反映实形的投影中,保持平面不动,只将直线AD绕垂直于平面△ABC所平行投影面的轴(一条垂直轴)旋转,将直线AD旋转成另一投影面平行线,在这个直线AD所平行的投影面中,直线AD与平面△ABC的夹角θ就可直接反映出来。
作图:如图4.28(a)所示。
①第一次旋转,将平面△ABC旋转成垂直面。在△ABC上作一条水平线AE,绕不指明的铅垂轴将它旋转成正垂面,此时,直线AD随之进行旋转。
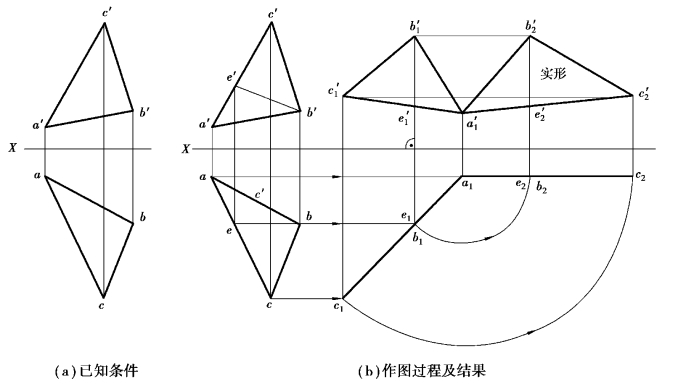
图4.27 求一般位置平面△ABC的实形
②第二次旋转,再将平面△ABC旋转成平行面。将第一次旋转中平面△ABC具有积聚性的投影,绕过C点的正垂轴旋转,把平面△ABC旋转成水平面,此时,直线AD也随之进行旋转。
③第三次旋转,保持平面不动,只将直线AD绕过A点的铅垂轴旋转,使直线AD旋转成正平线。此时,直线AD反映实长的投影a3′d3′与平面△ABC具有积聚性的投影a′2b′2c′2之间的夹角,即为题目所求的夹角θ。
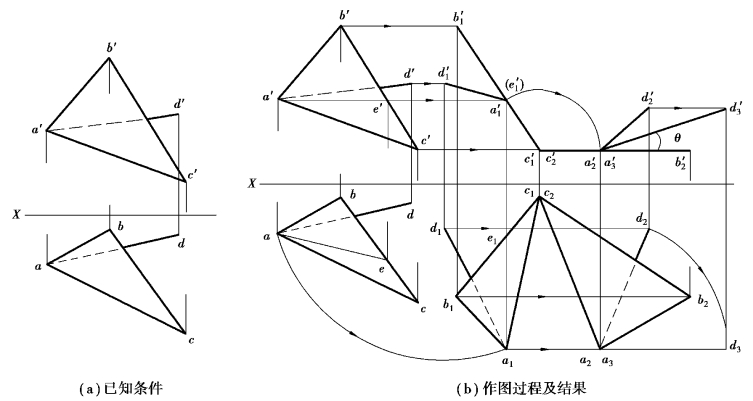
图4.28 求直线AE与平面△ABC的夹角θ
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




