画法几何与阴影透视：使用换面法解决定位和度量问题

1）一次换面的运用

在换面法中，新投影面的设置是十分重要的。下面结合几个例子说明用一次换面解决空间几何元素间定位和度量问题时，如何设置新面。从前面的分析中我们得知：新投影面必须垂直原投影面之一；新面的设置必须有利于解题。在投影图上，新面的设置是体现在画新轴的位置上的。

【例4.1】如图4.5（a）所示，求一般位置直线AB的实长及其倾角α。

【解】分析：当直线AB为正平线时，AB的正投影就反映实长，同时，正投影与投影轴的夹角反映直线AB的α倾角。所以，在考虑本例的变换过程中，应将直线AB变换成正平线，如图4.5（a）所示。从中不难看出，用新的V1面代替V面，使V1面平行于直线AB的同时垂直于H面。注意：该图中新轴与保留投影之间的关系是：新轴平行于保留投影，即X1∥ab。

作图：如图4.5（b）所示。

①作新轴X1∥ab。

②过保留投影a、b作新轴垂线。

③量取a′1ax1=a′ax，b′1bx1=b′bx，从而获得A、B两点在V1面上的新投影a′1、b′1。

④连接a′1、b′1，得直线AB的新投影，此时a′1b′1反映实长，它与X1轴的夹角即为直线AB的倾角α。

图4.5　求一般位置直线AB的实长及其倾角α

注意：在图4.5（b）所示的作图过程中，X1轴只需保持与ab平行，两者间的距离对于求AB直线的实长及倾角是没有影响的。

【例4.2】如图4.6所示，求铅垂面△ABC的实形。

【解】分析：从图4.6（a）中可以看出，需设置新投影面V1代替原投影面V。由于△ABC是铅垂面，所以V1面在平行于△ABC的同时一定要垂直于H面。注意：此图中新轴与铅垂面积聚投影的关系是：新轴平行于铅垂面积聚投影，即X1∥abc。

作图：如图4.6（b）所示。

①作新轴X1∥abc（铅垂面的积聚性投影）。

②过保留投影a、b、c作新轴垂线。

③分别量取点的新投影到新轴距离等于点的旧投影到旧轴距离，得a′1、b′1、c′1，此时△a′1b′1c′1反映△ABC实形。

图4.6　求三角形ABC的实形

【例4.3】如图4.7所示，求点到水平线AB的距离L及其投影l、l′。

【解】分析：如设置新投影面垂直于直线AB，则直线AB在新面上投影积聚为一点，此时，点C的新投影亦是一个点，这两点间的距离就是所求点C到直线AB的距离；由于AB是正平线，所以，应保留V面，用新投影面H1代替原投影面H，H1面垂直于AB的同时一定垂直于V面。

作图：如图4.7（b）所示。

①作新轴X1⊥a′b′；过保留投影a′、b′作新轴垂线，分别量取点的新投影到新轴距离等于点的旧投影到旧轴距离，求出直线AB的新投影a1b1（积聚性）。同理，可求出点C的新投影c1。

②积聚点a1b1与c1的连线l1即为所求距离的实长L。

③对于H1面，由于距离L是一条水平线，所以l′∥X1。

④根据距离的一个端点属于直线AB，即可求出l。

图4.7　求点到平行线（正平线）的距离

【例4.4】如图4.8（a）所示，求一般位置面△ABC的倾角α。

【解】分析：当把一般位置面变成垂直面后，倾角就可由垂直面的积聚投影与对应投影轴的夹角来获得。由于题目中要求的是α倾角，故H面应当保留。从前面章节的学习中我们得知，正垂面的正投影具有积聚性，它与投影轴的夹角反映该平面的α角。所以，需设置一个既与H面垂直又与△ABC垂直的V1面代替V面。如图4.8（a）立体图中所示，如果在△ABC上作一条水平线AD，使V1面垂直于水平线AD，这样就保证了新建V1面既垂直于△ABC又垂直于H面。

作图：如图4.8（b）所示。

①在△ABC中作一条水平线AD，先由a′d′∥X，作出ad。

②作新轴X1⊥ad，由换面法的作图步骤，求出△ABC的新投影a′1b′1c′1，此投影具有积聚性。

③积聚性投影a′1b′1c′1与X1轴的夹角反映△ABC的α倾角。

图4.8　求平面的水平倾角

【例4.5】如图4.9（a）所示，求直线EF与△ABC的交点K。

【解】分析：由前例可知，若将△ABC变换成垂直面，则新投影具有积聚性，此时可由平面的积聚性投影，直接求出它与直线的交点。从题目的条件中可看出，△ABC的AB边是水平线，所以需要建立新投影面V1垂直于AB。

作图：如图4.9（b）所示。

①由于△ABC中的AB是水平线，所以作新轴X1⊥ab，便可将△ABC变换成正垂面。此时直线EF应随之进行投影变换。

②根据换面法作图步骤，求出△ABC及直线EF的新投影a′1b′1c′1（积聚性）及e′1f′1。此时，便可直接获取交点k′1。

③将k′1返回到原投影体系中，由点K从属于直线EF，得k及k′，便求出了交点的投影。

④判断出可见性即完成题目的要求。

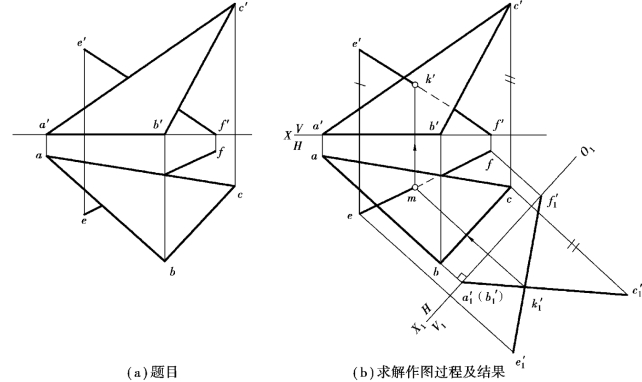
图4.9　求直线EF与△ABC的交点(www.xing528.com)

2）二次换面法的运用

【例4.6】如图4.10（a）所示，求一般位置平面△ABC的实形。

【解】分析：若直接设置新投影面平行△ABC，则新投影反映△ABC实形。但由于△ABC是一般位置面，与它平行的新投影面也一定是一般位置面，不能与原体系（V/H）之一的V面或H面构成相互垂直的新体系。从例4.2可知，垂直面可以通过一次换面成为平行面，从而反映实形；又从例4.4可知，一般位置面可以通过一次换面成为垂直面，因此得到启示：先将一般位置面经一次换面变换成垂直面，再将垂直面经第二次换面变换成平行面，从而可获得△ABC的实形。

作图：如图4.10（b）所示。

①在△ABC中作出正平线AD，即作ad∥X，再由d→得d′。

②作一次换面的新轴X1⊥a′d′。

③由换面法作图步骤，求出△ABC一次换面后在H1面上的新投影a1b1c1（具有积聚性）。

④再作二次换面的新轴X2//a1b1c1，再由换面法作图步骤求出△ABC在V2面上的新投影△a′2b′2c′2，该投影即反映△ABC的实形。

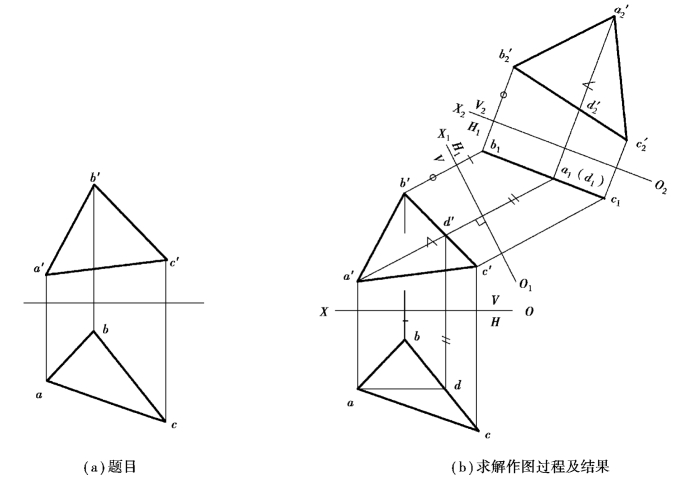
图4.10　求一般位置平面△ABC的实形

【例4.7】如图4.11（a）所示，求点C到一般位置直线AB的距离CD及投影cd、c′d′。

【解】分析：从前面例4.1及例4.3的求解中知道，当把一般位置直线变换成垂直线时，点到直线的距离在积聚投影中可直接反映出来。如图4.11（a）所示，一般位置直线只能先变换成平行线后，才能再次变换成垂直线；在直线的二次变换过程中，点C是随之进行变换的。

作图：如图4.11（b）所示。

①作一次换面的新轴X1//ab，将直线AB变换成一平行线（正平线），此时点C随之变换。

②由换面法作图步骤，求出直线AB在V1面的新投影a′1b′1及c′1。

③再作二次换面的新轴X2⊥a′1b′1，使直线AB变换成垂直线（铅垂线），此时点C也随之变换。

④再由换面法作图步骤，求出直线AB及点C在H2面上的投影a2b2（积聚性）及c2，将积聚点a2b2与c2连线，即获得所求点C到直线AB的距离CD在H2面上的投影c2d2。c2d2反映距离CD的实长。

⑤由于CD⊥AB，故在V1/H2体系中直线CD为H2面的平行线。作c′1d′1//X2，再由点D从属于直线AB，就可逐步返回求出直线CD的H面及V面投影。

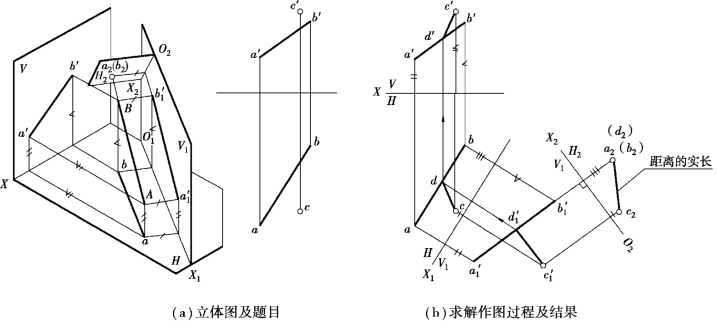
图4.11　求点到一般直线的距离

【例4.8】如图4.12（a）所示，已知由四个梯形平面组成的漏斗，求漏斗相邻两平面ABCD和CDEF的夹角θ。

【解】分析：如图4.12（b）所示，只要将两平面同时变换成同一投影面的垂直面，也就是将它们的交线CD变换成投影面的垂直线时，两个平面积聚投影线段间的夹角就反映出这两个平面间的真实夹角；由于平面ABCD与平面CDEF的交线是一般位置直线CD，由前例知道，要将它变换成垂直线需要经过两次变换。由于直线及直线外一点可确定一个平面，所以对于平面ABCD和平面CDEF，只需变换共有的交线CD以及平面ABCD上的点A和平面CDEF上的点E，无须变换整个平面。

作图：如图4.12（c）所示。

①作一次换面的新轴X1∥c′d′，根据换面法的作图步骤，求出c1、d1、b1、e1并连接c1d1。此时，共有的交线CD变换成了平行线（水平线）。

②作二次换面的新轴X2⊥c1d1，根据换面法的作图步骤，求出c′2、d′2、a′2、e′2。这时c′2、d′2具有积聚性，它与a′2、e′2的连线即为平面ABCD和平面CDEF的积聚投影，即反映出了两平面的夹角θ。

图4.12　求相邻两平面的夹角θ

【例4.9】如图4.13（a）所示，正方形ABCD的顶点A在直线SH上，顶点C在直线BE上，请补全正方形ABCD的两面投影。

【解】分析：因为正方形相邻两边相互垂直并相等，其中BC边在直线BE上，所以需经过一次换面，将直线BE变换成平行线。此时，可按一边平行于投影面的直角的投影特性，求出BC边相邻边AB的投影。在一次换面后的投影体系中，AB边仍为一般位置直线，故应再作第二次换面，只将AB边变换成平行线，这样就求出了正方形的边长。在直线BE反映实长的投影中，由AB等于BC，便可确定出C点。

作图：如图4.13（b）所示。

①将直线BE变换成平行线，求出顶点A和AB边。作一次换面的新轴X1∥be，根据换面法的作图步骤，求出b′1、e′1、s′1、h′1，并且连接b′1e′1和s′1h′1线段。此时，已将直线BE变换成了正平线，由直角投影定理作a′1b′1⊥b′1e′1，求出点a′1及线段a′1b′1。

图4.13　补全正方形ABCD的投影

②进行第二次换面，此时，只需将AB边变换成平行线。作新轴X2∥a′1b′1，根据换面法的作图步骤，求出线段a2b2，它为反映正方形边长的实长投影（即AB=a2b2）。

③由a2b2=b′1c′1（即AB=BC），得到c′1点，再由点C从属于直线BE、点A从属于直线SH，逐次返回原投影体系中。根据正方形的几何性质——对边平行并且相等，便可求出正方形ABCD的投影。

【例4.10】如图4.14所示，已知点K到△ABC的距离为10mm，求点K的水平投影k。

【解】分析：从前面的例4.4中我们知道，一般位置平面可以经过一次换面变换成为垂直面；当平面在新投影面上的投影具有积聚性时，平面外一点到平面的距离，就会在平面具有积聚性的投影中直接反映出来。

作图：如图4.14（b）所示。

①进行一次换面，将△ABC变换成投影面的垂直面。先在△ABC上作水平线AD，作新轴X1⊥ad，根据换面法的作图步骤，作出△ABC在新投影面V1上的投影a′1b′1c′1。此投影具有积聚性，K点在V1面上的投影只能根据K点的旧投影到旧轴的距离等于新投影到新轴的距离，画出一条平行于X1轴的直线l′1。

②根据已知条件K点到△ABC的距离等于10mm，在△ABC具有积聚性的投影面（V1面）上，作与积聚性投影a′1b′1c′1相距10mm的平行线（可作出两条），这两条平行线与前面作的平行于X1轴的平行线l1′相交，就是K点在V1面上的新投影k′1。

③由k′1向X1轴作垂线并延长，它与由k′向X轴所作垂线的交点，就为K点的水平投影k。

④由于第②步骤所作的距离等于10mm平行线有两条，所以该题有两解。

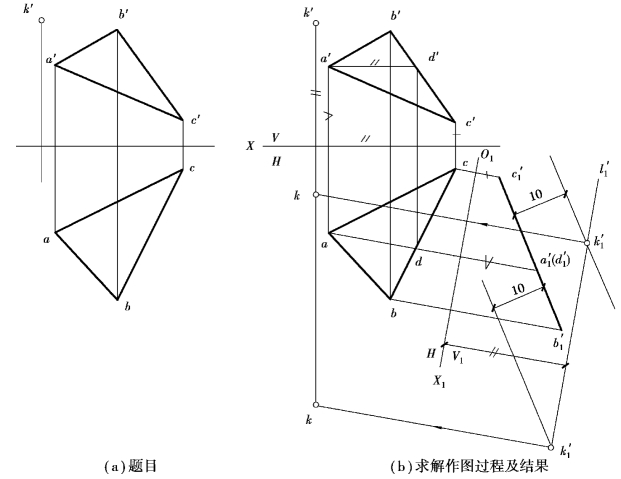
图4.14　已知点K到平面的距离为定长10，求水平投影k