画法几何与阴影透视-综合举例

【例3.15】如图3.39（a）所示，过点K作一平面既与直线MN平行，又与平面ABC垂直。

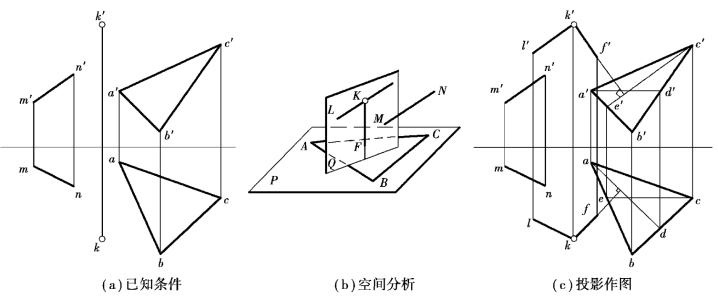
图3.39　过点K作一平面既与直线MN平行又与平面ABC垂直

【解】分析：要求所作平面平行于直线MN，只需要保证该面包含一条平行于MN的直线；同时，平面垂直于另一平面，只需要保证其中包含另一平面的垂线。本题对平面的表达方式没有特殊限定，因此只需要过已知点K分别作满足上述条件的两条直线，以相交直线的形式表达的平面即为所求[图3.39（b）]。

作图：如图3.39（c）所示。

①过点K作直线KL∥MN。投影作图步骤为：分别过k′，k作k′l′∥m′n′，kl∥mn。

②过点K作直线KF⊥△ABC。投影作图步骤为：分别在平面ABC上取出水平线AD与正平线CE，分别过k′、k作k′f′⊥c′e′，kf⊥ad。

KL与KF所表达的平面即为所求。

检查、讨论：检查从略。此题只需要作出垂直于△ABC的直线的方向，并不需要求出准确的垂足位置，因此F点可以是垂线上任意一点。

【例3.16】如图3.40（a）所示，作一直线MN与相叉直线AB和CD相交，并平行于直线EF。

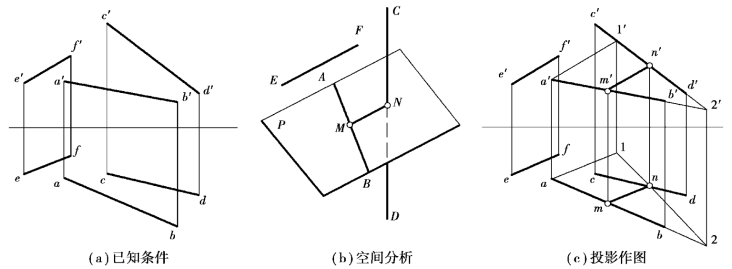
图3.40　作直线MN平行于直线EF并与两交叉直线AB、CD均相交

【解】分析：要求作直线MN平行于EF，且相叉直线AB、CD均相交。如果用轨迹分析法进行空间分析，先少考虑一个要求，与已知直线AB相交并和已知直线EF平行的直线的轨迹是一个包含AB且平行于EF的平面。同理，与已知直线CD相交并和已知直线EF平行的直线的轨迹是一个包含CD且平行于EF的平面。要同时满足这两条几何轨迹的要求，所求直线MN必为上述两平面的交线。EF已确定MN的方向，故只需求得属于交线的一个交点即可。所以，空间作图步骤为：过AB（或CD）作平面平行于EF（图中过点A作直线AL平行于EF，AL和AB所确定的平面平行于EF）；再求此平面与另一直线CD的交点M；最后过N作MN平行于EF，交AB于N，MN为所求直线[图3.40（b）]。

作图：如图3.40（c）所示。

①过直线AB上点A作直线AL∥EF。分别过a′、a作a′l′∥e′f′，al∥ef。相交直线AB、AL确定的平面平行于EF。

②求CD与上述平面的交点M。含CD作正垂面R为辅助面，RV与c′d′重合，在V投影上直接确定辅助面R与上述平面交线的V投影1′2′，由1′2′求出12。12与cd的交点m即为点M的H投影，由m求出m′。

③过点M作直线MN∥EF。过m作mn∥ef，且交ab于n，再过m′作m′n′∥e′f′，且交a′b′于n′。作图时要注意nn′必须垂直于投影轴OX，MN（mn，m′n′）即为所求直线。

检查、讨论：检查从略。按空间分析，本题还有另一种作图方法，即过相叉直线AB、CD分别作平面平行于直线EF，求出两平面的交线即得所求直线。此题和图3.38中过点E作一直线与两交叉直线AB、CD均相交一题属同一类型，思路相同。只是限定所求直线不同，一个是通过同一点，而另一个是平行于同一直线。

【例3.17】如图3.41（a）所示，求作以AB为底，顶点C属于直线MN的等腰三角形ABC。(www.xing528.com)

【解】分析：用相对位置关系分析法进行分析。如图3.41（b）所示，如果等腰△ABC已作出，其顶点C既属于AB的中垂面，又属于直线MN，所以顶点C必为AB的中垂面与MN的交点。

作图：如图3.41（c）所示。

①作AB的中垂面P。过中点D分别作与AB垂直的正平线DⅠ和水平线DⅡ，所确定的平面P为AB的中垂面。

②求MN与所作中垂面P的交点。为此，含MN作辅助正垂面Q，求辅助面Q与中垂面P的交线ⅠⅡ（1′2′，12）。12与mn的交点c即为等腰△ABC的顶点C的H投影，由c作出c′。

图3.41　作等腰△ABC

③分别连接△a′b′c′，△abc，△ABC即为所求等腰三角形。

检查、讨论：检查从略。此题要求还可能有其他说法，例如，求MN上一点C，使其到线段AB两端点A、B距离相等；求MN上一点C，使AB分别与CA、CB的夹角均相等；求作以AB为对角线，顶点C属于MN的菱形等，但其分析、作图均与本例相同。

【例3.18】如图3.42（a）所示，作一平面P，使其与△ABC平行，且距△ABC为定长L。

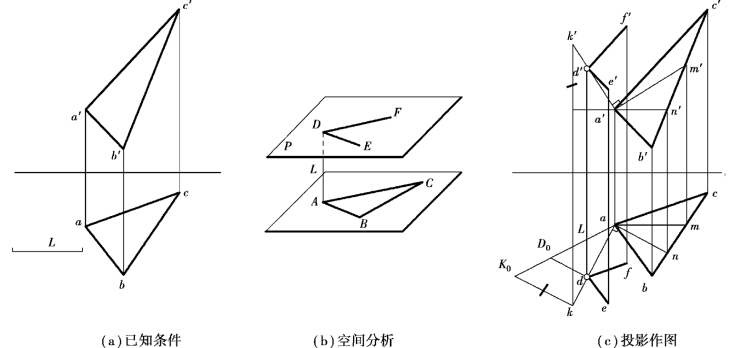
图3.42　作与已知平面距离为定长L的平行平面

【解】分析：仍用相对位置关系分析法。如图3.42（b）所示，假定所求平面P已作出，则相互平行的平面P和△ABC之间的任一垂线实长为L，故只要在这样的垂线取定长L。例如，在过顶点A的垂线上AD=L，然后过点D作平面P平行于△ABC即可。

作图：如图3.42（c）所示。

①过点A作△ABC的垂线AK。先作属于△ABC的正平线AM和水平线AN，然后过a作ak⊥an，过a′作a′k′⊥a′m′，K点可以为垂线上的任意一点。

②在△ABC的垂线AK上取点D，使AD=L。先用直角三角形法求AK的实长，然后用定比确定D。最后确定d′、d，在AK的实长aK0上量取aD0=L，过D0作D0d∥K0k交ak于d，由d求出d′。

③过点D作平面P平行于△ABC（用相交直线表示较简单）。过d作de∥ab，df∥ac；再过d′作d′e′∥a′b′，d′f′∥a′c′，由DE（de，d′e′）和DF（df，d′f′）确定的平面P为平行于△ABC且距离为L的平面。

检查、讨论：检查从略。本题有两解，另一解在△ABC的另一侧距离为L处。另外，本题涉及一个重要的基本作图，即在一条定直线上利用定比确定所需要的点。