综合问题解决步骤及几何透视原理简介

综合性的空间几何问题比较复杂，需要同时满足几个要求，求解它们的一般步骤为：分析、作图、检查、讨论。

（1）分析

作图前的分析内容大致有：弄清题意，明确已知条件有哪些，需要求解什么。把需要求解的问题放到空间里去解决，想象出已知条件在空间的状态（即所谓的空间分析），拟订空间作图步骤或曰解题方案。注意尽量应用在画法几何中已有的相应结论，例如与铅垂面垂直的直线一定是水平线等，见表3.1和表3.2。

表3.1　两特殊位置平面相交

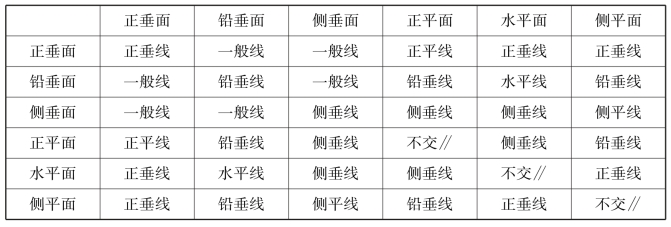
表3.2　特殊位置平面与直线垂直

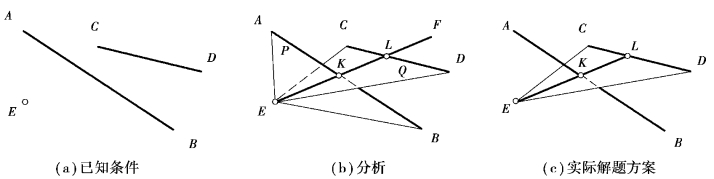
空间分析有相对位置关系分析法和轨迹分析法两种方法。前者假设题目所要求的几何元素已作出，将其加入题目给定的几何元素中，按照题目所要求的各个条件逐一分析它们之间的相对位置和从属关系，探求几何元素的确定条件，从而获得空间解题方案；后者根据题目给定的若干条件，逐条运用空间几何轨迹的概念，分析所求几何元素在该条件下的空间几何轨迹，然后综合这些单个条件下的几何轨迹，从而得出空间解题步骤。如图3.38（a）所示，过点E作一条直线与两交叉直线AB、CD均相交，分别用空间分析的两种分析法进行分析。

(www.xing528.com)

图3.38　过已知点E作一直线与两交叉直线AB、CD均相交

①相对位置关系分析法：假定所求直线EF已作出，直线EF与已知直线AB相交于点K，则EF必然属于点E和直线AB所确定的平面P。同理，EF必然属于点E和直线CD所确定的平面Q，故所求直线EF为平面P、Q的交线[图3.38（b）]。

②轨迹分析法：过点E与直线AB相交的直线的轨迹是由定点E和直线AB所确定的平面P。同理，过点E与直线CD相交的直线的轨迹是由定点E和直线CD所确定的平面Q。能同时满足这两条几何轨迹要求的，只有平面P、Q的交线[图3.38（b）]。

由于已有共有点E，所以只需再求一点即可。实际解题方案为：连接EC、ED得△ECD，然后求AB与△ECD的交点K，再连接并延长EK交CD于点L。EL即为所求直线[图3.38（c）]。

（2）作图

在已有空间解题方案的基础上，分清投影作图步骤。有时，空间作图的一步需要几个基本投影作图才能完成，所以一定要明确投影作图步骤后，方可开始作图。

（3）检查、讨论

检查几何条件是否成立，有无过失性错误等方面内容。例如，判别可见性以后，可用三角板、铅笔等模拟空间相交情况来验证正确与否。讨论一般是考虑在现有题设条件下可能有几解，局部变动个别条件会引起作图的哪些变化等。总之，通过解答题目，为巩固投影理论知识，增强空间想象能力，尽可能地展开一些认知思维活动，可达到事半功倍的效果。