画法几何:一般位置平面与特殊位置平面相交

两平面的相交问题重点在于求得交线并判定可见性。

两平面的交线是直线，是相交两平面的共有线，只要求得属于交线的任意两点，直接连接即得。对于闭合的平面多边形，仍然存在着各边线的虚实判断，根据两平面关系不同，可以分为全交和互交两种形式（图3.16）。平面Q全部穿过平面P，称为全交，交线的端点全部出现在平面Q的边线；P、Q两平面相互咬合，交线端点分别出现在两平面各自的一条边线上，称为互交。

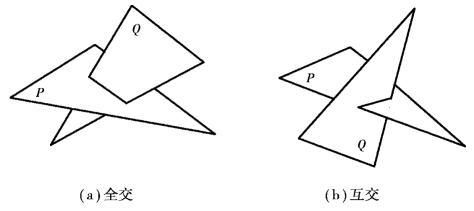
图3.16　平面图形的全交和互交

当其中一个平面处于特殊位置时，其交线可以利用积聚性简便地作出。图3.17（a）所示为一般位置平面和铅垂面相交。显然，按照3.2.1中相应方法分别作出属于△ABC的AB、AC与铅垂面ⅠⅡⅢⅣ的交点K、L，然后连接K、L即为交线。

作法具体如下：

（1）求交线

①求AB与平面ⅠⅡⅢⅣ的交点K。在H投影上过ab与12（3）（4）的交点k向上作投影联系线交a′b′于k′；

②按照同样的方法作出AC与平面ⅠⅡⅢⅣ的交点L。

③连接k′l′，KL（kl、k′l′）为所求交线。(www.xing528.com)

（2）判别可见性

交线KL的两面投影永远为可见，直接画为实线，需要判别的是平面边线的相互遮挡问题。铅垂面ⅠⅡⅢⅣ中，其H面投影积聚为一条直线，故H面投影中不存在边线的相互遮挡，不需要判别可见性，为实线。判别V面投影中的虚线部分，有两种方法：

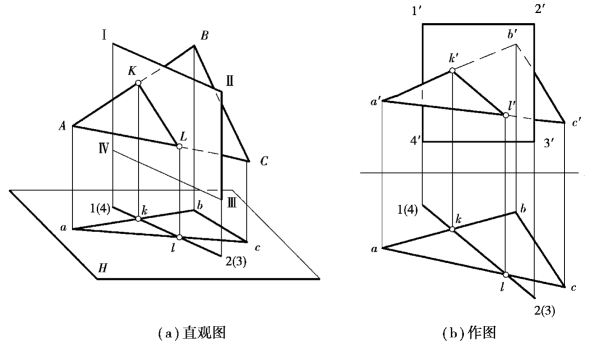
图3.17　一般位置平面与投影面垂直面相交

①重影点判断法。利用交叉两直线的重影点来进行判断。图3.17（b）中，在1′4′，2′3′与a′b′，a′c′的4个投影交点中任选一个，如1′4′和a′b′的投影交点向下作投影联系线至H投影，先遇14，故1′4′在k′a′之后，重合部分不可见，投影重合部分为虚线，k′a′可见，为实线。平面是连续的，因此在V投影中k′l′b′c′一侧两个图形重叠的部分，属于△ABC的图形都为不可见，其图线均为虚线，属于ⅠⅡⅢⅣ的图线为实线。k′l′a′一侧两个图形重叠的部分，图线的虚实与k′l′b′c′一侧相反。

②简单观察法：在H投影图上以交线KL为界，分△abc为左右两部分，左侧kla在1234之前，其V投影k′l′a′可见，应为实线，而1′2′在后，重合部分该画虚线。右侧可见性与左侧相反，不再赘述。

③虚实相间法进行全图验证

两平面相交的问题作图过程相对复杂，涉及虚实性判别的图线比较多，作图完成后要用“虚实相间法”再次进行全图的关系验证。无论平面关系是全交还是互交，必然会出现两类关键点：两个交线端点、若干两平面边线投影相交位置点。在无积聚投影的情况下，它们均为可见部分与不可见部分的分界点，即“虚实分界点”。每过这样的点，平面边线的虚实性就会发生一次变化，呈现一个“虚→实→虚→实”的循环状态。正确的交线作图和可见性判断，会使面投影出现完整的虚实循环。假若发现应该变为虚线时，所作图线仍是实线，则作图必然出现了错误，应逐项检查，找到问题并更正。

这里要特别注意b′点所在位置。b′点本身被另一个平面的投影完全遮挡，并不是虚实分界点，其两侧的图线都是虚线。因此，虚实分界点并不包括平面图形的顶点。