直线与平面的平行关系

空间几何元素的平行问题都可以理解为二者相交于无限远点。而直线与平面如果有从属关系，则可理解为二者有无穷多个交点。直线与平面的平行或者相交，也应在直线不属于平面的前提下讨论。

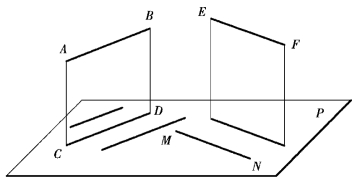
图3.1　直线与平面平行

1）几何条件

若一直线与属于平面的另一直线平行，且直线不属于该平面，则直线与该平面平行。反之，若一直线与某平面平行，则过属于平面的任意一点都可作出与该直线平行的直线。

图3.1中，直线AB在平面P之外，同时与属于平面P的直线CD相平行，则直线AB平行于平面P，在平面P中可以取出无数条平行于AB的直线。另一直线EF平行于平面P，则过属于平面P的任意一点M可作出直线MN平行于直线EF，同时MN属于平面P。

2）投影作图

根据上述几何条件，可以解决两类常见的投影作图问题：一是作直线平行于某一平面或者作平面平行于已知直线；二是判断直线与平面是否平行。根据直线或平面与投影面的相对位置关系是否特殊，这两类投影作图问题又可分成一般情况和特殊情况。

（1）特殊情况——直线与特殊位置平面平行

平面与投影面具有特殊位置关系时，会出现至少一个积聚投影，此积聚投影成为解题入手点。若直线平行于特殊面，则平面的积聚投影一定与直线的同面投影平行，且两者间距等于直线与特殊位置平面的距离（图3.2）。

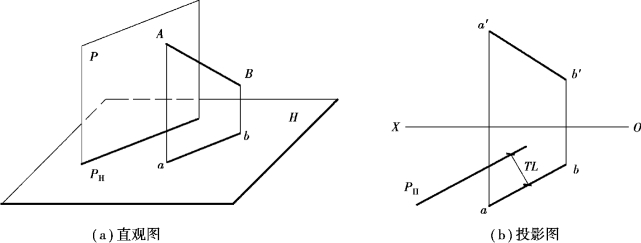
图3.2　直线与垂直面平行

【例3.1】过已知点K作铅垂面P和正垂面Q（迹线表示）平行于已知直线AB，如图3.3（a）所示。

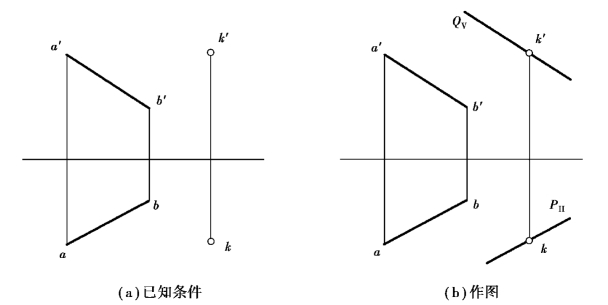
图3.3　过点K作铅垂面P∥AB和正垂面Q∥AB

【解】分析：P⊥H，PH有积聚性，所求P∥AB只需PH∥ab即可；Q⊥V，QV有积聚性，所求Q∥AB只要保证PV∥a′b′即可。

作图：如图3.3（b）所示。

①在H投影中过k作PH∥ab，ab和PH间的距离为直线AB与铅垂面P间的距离。

②在V投影中过k′作QV∥a′b′，a′b′和QV之间的距离为直线AB和正垂面Q之间的距离。

注意：这里的PH与QV分别是两个不同平面的迹线，并不是同一条直线的两面投影。

【例3.2】过已知点K作直线KL平行于已知平面△ABC，如图3.4（a）所示。(www.xing528.com)

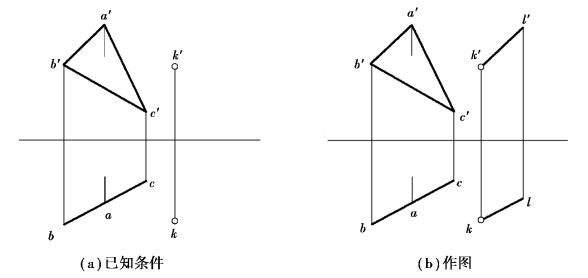
图3.4　过点K作直线KL∥平面△ABC

【解】分析：KL∥平面△ABC，只需KL为平面中任意一条直线的平行线即可。平面中存在方向不同的无数条直线，故此题有无穷多解。已知平面的H面投影积聚为一条直线，故为铅垂面。因此，只需保证PL的水平投影与平面的积聚投影平行，另一个投影可任意作。

作图：如图3.4（b）所示，作pl∥ab，p′l′∥a′b′，KL为满足题目要求的答案之一。

（2）一般情况——直线与一般位置平面平行

一般位置平面的各面投影均不具有积聚性，判断直线是否与其平行，必须要对照各面投影，利用直线与平面平行的几何条件，寻找平面中是否存在与已知直线平行的直线。

【例3.3】过已知点M作正平线MN平行于已知平面△ABC，如图3.5（a）所示。

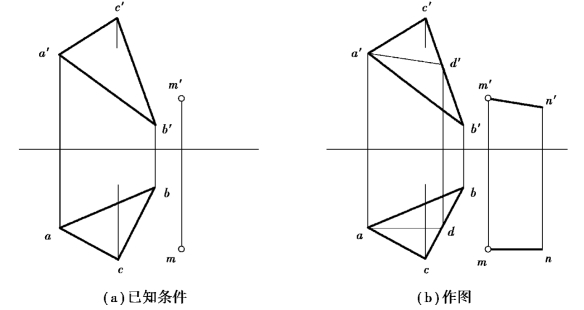
图3.5　过点M作正平线MN∥平面△ABC

【解】分析：△ABC为一般位置平面，要求所作MN既平行于V面，又平行于平面△ABC，则MN应平行于平面△ABC与V面的交线，即平面△ABC的V面迹线，也是属于平面△ABC的正平线的方向。同时，从例3.2中已经分析得知，无论平面处于何种位置，过点M可作无数条直线平行于已知平面△ABC，但却只有一条是正平线。可见，首先需作属于平面△ABC的正平线。

作图：如图3.5（b）所示。

①作属于平面△ABC的正平线AD。在H投影中过点a作ad∥OX，与bc相交于点d，求得d点的V面投影d′。连接a′d′，得AD的两面投影。

②过点M作直线MN与AD平行。在H投影中过m作mn∥ad∥OX，在V投影中过m′作m′n′∥a′d′，MN为所求正平线。

【例3.4】试判别直线KL是否平行于平面△ABC，如图3.6（a）所示。

【解】分析：△ABC为一般位置平面，KL若与其平行，必然在△ABC中能够取出与之平行的直线。解决此类问题，需要尝试在已知平面中作直线的平行线。若能作出，两者平行；反之，则不平行。

作图：如图3.6（b）所示，在V投影中过a′作a′d′∥k′l′，与b′c′相交于d′，作出AD的水平投影ad。ad与kl不平行，故KL与平面△ABC不平行。

综上所述，当直线与特殊位置平面平行时，该平面具有积聚性的投影和直线同面投影必然平行，其间距就是直线与特殊位置平面之间的实际距离，作图时不必作辅助线。讨论直线与一般位置平面的平行关系时，其投影没有明显的特征，投影作图都必须归结为两直线的平行问题，需要先作辅助线。因此，作图前必须先对平面的位置进行分析，判断其是否具有积聚投影，以便快速准确地完成题目。

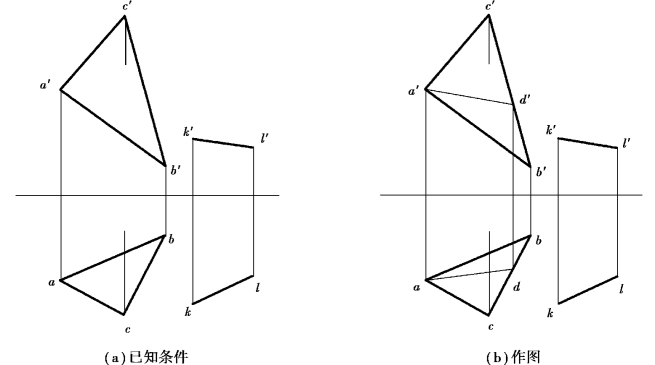
图3.6　判别直线KL与平面△ABC是否平行