平面投影表示法:画法几何与阴影透视

1）用几何元素表示平面

根据初等几何可以知道，决定一个平面的最基本的几何要素是不在同一直线上的三点。因此，在投影图中，可以利用这一组几何元素的组合的投影来表示平面的空间位置。

①不属于同一直线的三点，如图2.42（a）所示；

②一条直线和该直线外的一点，如图2.42（b）所示；

③相交二直线，如图2.42（c）所示；

④平行二直线，如图2.42（d）所示；

⑤任意平面图形，如图2.42（e）所示。

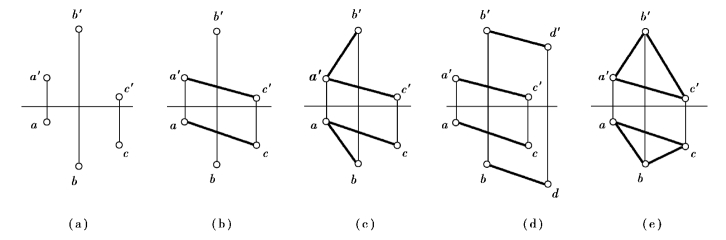
图2.42　几何元素表示平面

如图2.42所示，欲在投影图上确定出一个平面，只需给出上述各组元素中任何一组投影就可以了。显然，上述各组元素是可以相互转换的。例如，将图2.42（a）的A、C两点连接起来便可以换为图2.42（b）的形式，连接图2.42（b）的A、B两点便又将其转换为图2.42（c）的形式了。但无论怎样转换，所转换的平面在转换前后都是同一平面，只是形式不同而已。(www.xing528.com)

2）用平面的迹线表示平面

根据前面的讲述可知，一条直线与投影面的交点称为迹点。一平面与投影面相交，其交线称为平面的迹线。平面与V面相交的交线称为正面迹线（常用PV表示），与H面相交的交线称为水平迹线（常用PH表示），与W面相交的交线称为侧面迹线（常用PW表示）。相邻投影面的迹线交投影轴于一点，此点称为迹线的集合点，分别用PX、PY、PZ表示（图2.43）。迹线通常用粗实线表示；当迹线用作辅助平面求解画法几何问题时，迹线则用细实线（或者两端是粗线的细线）表示。

从图2.43中可以看出，在三面投影体系中，PV为V面上的直线，其正面投影与迹线本身重合，而其水平投影及侧面投影分别重合于OX轴与OZ轴。习惯上，采用迹线本身做标记，而不必再用符号标出它的其他二面投影，水平迹线PH与侧面迹线PW与此相同。

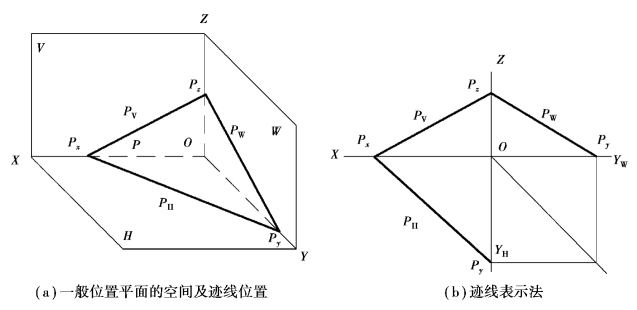
图2.43　用迹线表示平面

用几何元素表示的平面可以转换为迹线表示的平面，其实质就是求作属于平面上的任意两直线的迹点问题。如图2.44所示，取平面上任意二直线（如AB与BC），作出直线的水平迹点点D与点F，点D与点F必属于平面△ABC与H面的交线PH，故而连接点D与点F即得PH。同理，求出两直线AB与BC的正面迹点E、G，可得PV。

图2.44　非迹线平面转换为迹线平面