直角投影定理：画法几何与阴影透视的成果

两相交直线（或两相叉直线）之间的夹角，可以是锐角，也可以是钝角或直角。一般说来，要使一个角不变形地投射在某一投影面上，必须使此角的两边都平行于该投影面。通常情况下，空间直角的投影并不是直角，反之，两条直线的投影夹角为直角的空间直线之间的夹角一般也不是直角。但是，对于相互垂直的两直角边，只要有一边平行于某投影面，则此直角在该投影面上的投影仍旧是直角。

如图2.36所示，第一种情况是，相互垂直的两直角边AB和BC都平行于H面，则在H面上直接反映直角是毋庸置疑的，如图2.36（a）。第二种情况是，当空间直角ABC的一边AB平行于H面，而另一边BC与H面倾斜时，因为AB既垂直于BC，又垂直于Bb，所以AB垂直于投射面BCcb。又知AB和它的投影ab是互相平行的，所以ab也同样垂直于投射面BCcb。由此证得ab丄bc，即∠abc=90°，如图2.36（b）。这就是一边平行于投影面直角的投影定律，即：当构成直角的两条直线中，有一直线是投影面的平行线，则此两直线在该投影面上的投影仍然反映成直角；反之，如果两直线的同面投影构成直角，且两直线之一是该投影面的平行线，则可断定该两直线在空间相互垂直。要注意的是，该直角∠ABC在V面的投影∠a′b′c′≠90°。

上述结论既适用于相互垂直的相交两直线，又适用于相互垂直的相叉两直线，如图2.36（c）中A1B1与CB就是相互垂直交叉的两条直线，同样存在前面所述的投影定律。

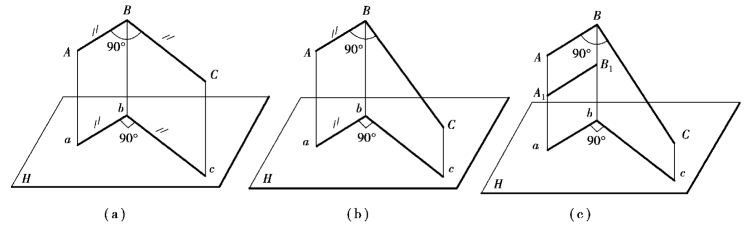
图2.36　一条边平行于投影面的直角的投影

图2.37所表示的相交两直线AB和BC及相叉两直线MN和EF，由于它们的水平投影相互垂直，并且其中有一条为水平线，所以它们在空间也是相互垂直的。同样，图2.38所示的相交两直线及相叉两直线，也是相互垂直的，因为它们的正面投影相互垂直，并且其中有一条为正平线。

直角投影的这种特性，常常被用于在投影图上解决有关距离的问题。

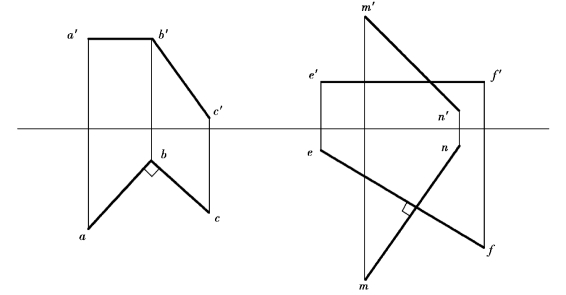
图2.37　交叉两直线其中一条边为水平线的直角投影

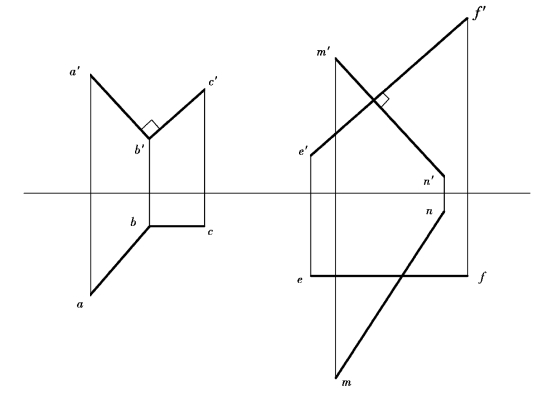
图2.38　一条边为正平线的直角投影

【例2.11】求图2.39中点A到铅垂线CD的距离。

【解】分析：点到直线的距离，是通过点向直线所引的垂线来确定的。由于所给的直线CD是铅垂线，所以它的垂线AB一定是一条水平线，它的水平投影反映实长。

作图：如图2.39所示。

【例2.12】求图2.40中点A到正平线CD的距离。

【解】分析：从图中可知，直线CD为正平线，通过A点向CD所引的垂线AB是一般位置直线，但根据直角的投影特性可知：a′b′⊥c′d′。(https://www.xing528.com)

作图：①过a′作投影a′b′⊥c′d′，得交点b′。

②由b′向下作垂线，在cd上得到b；连a和b，得到投影ab。

③用直角三角形法，作出垂线AB的实长ab0。

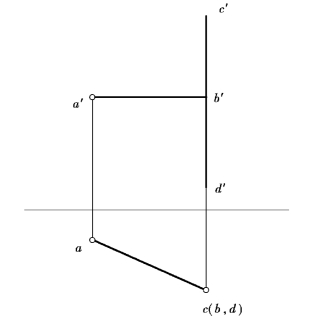
图2.39　求点到铅垂线的距离图

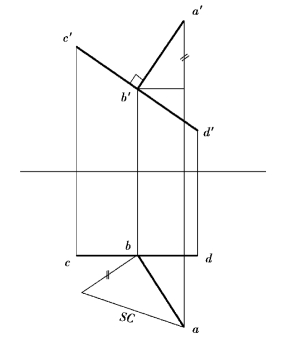
图2.40　点到正平线的距离

【例2.13】已知MN为正平线，如图2.41（a）所示。作直角等腰三角形△ABC，且BC为直角边，属于MN。

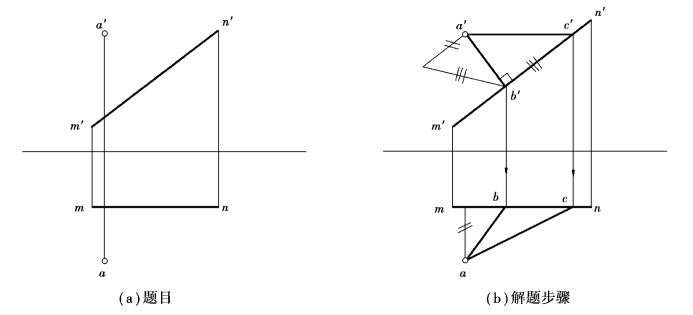
图2.41　综合题

【解】分析：△ABC为直角三角形，BC为直角边，则AB⊥BC，AB=BC；因为MN为正平线，根据直角定理可求出B点的投影。根据直角三角形法求出AB实长，BC属于MN，在m′n′上反映BC实长求得C点的投影。

作图：如图2.41（b）所示。

①过a′点作m′n′的垂线，交于b′点。由b′长对正得到b。

②根据AB的两面投影用直角三角形法求AB实长。

③在m′n′上量取b′c′=SCAB，求出c′，由c′长对正得到c。最后，加深线型。