一般位置直线的实长及对投影面的倾角|画法几何与阴影透视

对各投影面均成倾斜的直线称为一般位置直线。对于一条一般位置的直线段，它的各个投影的长度均小于线段本身的实长。

如图2.23所示，设线段AB与投影面H、V和W的倾角分别为α、β和γ。由于通过A、B两点的投影线Aa、Bb垂直于H面，所以有

ab=AB·cosα;

a′b′=AB·cosβ;

a″b″=AB·cosγ。

因为夹角α、β和γ都不等于零，也不等于90°，所以cosα、cosβ和cosγ都小于1。这就证明：一般位置线段的三个投影都小于线段本身的实长。

如何根据一般位置直线的投影来求出它的实长与倾角呢？我们先从立体图中来分析这个问题的解法。

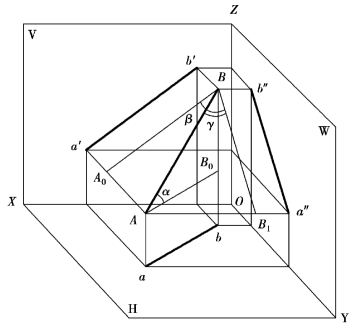
图2.23　直线的倾角

1）直线与H投影面的倾角α

在图2.24（a）中，过空间直线的端点A作直线AB0∥ab，得直角三角形AB0B，∠BAB0就是直线AB与H面的倾角α，AB是它的斜边，其中一条直角边AB0=ab，而另一条直角边BB0=Bb-Aa=ZB-ZA，ZA、ZB即为A、B两点的高度坐标，ZB-ZA为A、B两点的高度差。

根据立体图的分析可以得知，在直线的投影图上，我们可以作出与△AB0B全等的一个直角三角形，从而求得直线段的实长及其与投影面的倾角。其作图方法如图2.24（b）所示。

①过水平投影ab的端点b作ab的垂线。

②在所作垂线上截取bb0等于正面投影a′b′两端到OX轴的距离差ZB-ZA，得b0点。

③用直线连接a和b0，得直角三角形abb0，此时，ab0=AB，∠bab0=∠α。

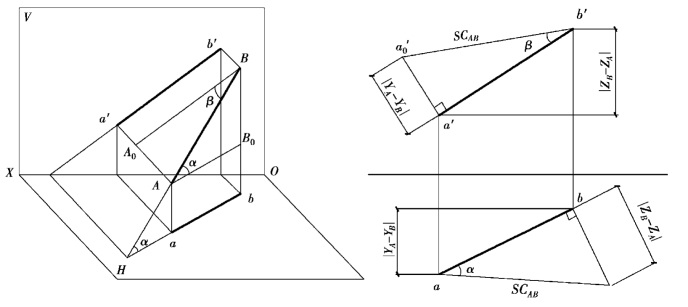
图2.24　用直角三角形法求一般位置直线的实长与倾角

2）直线与V投影面的倾角β

在图2.24（a）上过B点作直线BA0∥a′b′，A0点在投影线Aa′上，△ABA0为直角三角形，AB是它的斜边，AA0和BA0是它的两条直角边。此时，BA0=a′b′；而AA0=Aa′-Bb′=YAYB，即等于水平投影ab的两端到OX轴的距离差YA-YB。因此，用a′b′及距离差YA-YB为直角边作直角三角形，也能求出线段AB的实长。作法如图2.24（b）所示。所得的△a′b′a0′的斜边b′a0′等于线段AB的实长，但b′a0′与正面投影a′b′的夹角等于线段AB与V面的倾角β。

3）直线与W投影面的倾角γ(www.xing528.com)

γ角的求法与上面所述一样，如图2.23所示，作BB1∥a″b″，在直角三角形ABB1中，AB1为A、B两点之间的X坐标差，BB1的长度等于AB在W面上投影的长度，即a″b″，∠ABB1=γ。同样的道理，该直角三角形可以在投影图上表达出来。

综上所述，在投影图上求线段实长的方法是：以线段在某个投影面上的投影为一直角边，以线段的两端点到这个投影面的距离差为另一直角边，作一个直角三角形，此直角三角形的斜边就是所求线段的实长，而且此斜边和投影的夹角，就等于线段对该投影面的倾角。

从以上的分析和作图可以看出：我们通过作直角三角形来求线段的实长、倾角，故此法称为直角三角形法。直角三角形中的实长、距离差、投影长、倾角四者中任知其两者，便可以求出其余两者。而距离差、投影长、倾角三者均是相对于同一投影面而言。例如，我们要求某线段对H面的倾角、实长，应该知道该线段的H面投影以及线段两端点对H面距离差（坐标差），即Z坐标差。

值得注意的是，直角三角形法是一种在平面图上模拟空间的作图法，因此，可以在任何地方表达所需的直角三角形。

【例2.8】试用直角三角形法确定直线CD的实长及对投影面V的倾角β。

【解】分析：此题要求直线CD对V面的倾角，所以必须以CD的正面投影c′d′为一直角边。另一直角边则应是水平投影cd两端点到OX轴的距离差（Y坐标差）。

作图：①过水平投影c作X轴的平行线，与d′d交于d0，并延长该线。

②取d0c0=c′d′，将c0与d相连。

③此时，c0d=CD，∠c0=β，如图2.25所示。

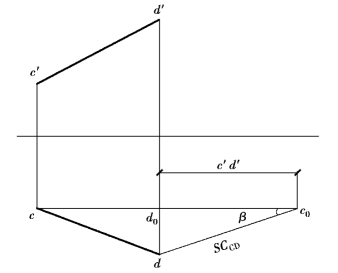
图2.25　求直线的真长和倾角

【例2.9】已知直线CD对投影面H的倾角α=30°，如图2.26（a）所示，试补全正面投影c′d′。

【解】分析：这是与前一例题性质相反的问题，给出倾角作投影。应该注意：如果要求直线CD对H面的倾角α，那么必须以水平投影cd为直角边，以正面投影c′d′两端的高度差为另一直角边，作直角三角形。虽然题中d′没有给出，但已知α=30°。所以这个直角三角形也可以作出（因为一个直角三角形可以由它的一条直角边及一个锐角所确定）。因此，就能确定c′d′两端的高度差，从而补全CD的正面投影。

作图：如图2.26（b）所示。

①过c′引OX轴的平行线，与过d向上作出的铅垂联系线相交，得d′0，并延长至c′0，使c′0d′0=cd；

②自c′0对c′0d′0作30°角的斜线，此斜线与过d的铅垂联系线相交于d′；

③连接c′和d′，得正面投影c′d′（由于不能确定D点在C点的上方还是下方，所以该题有两解）。

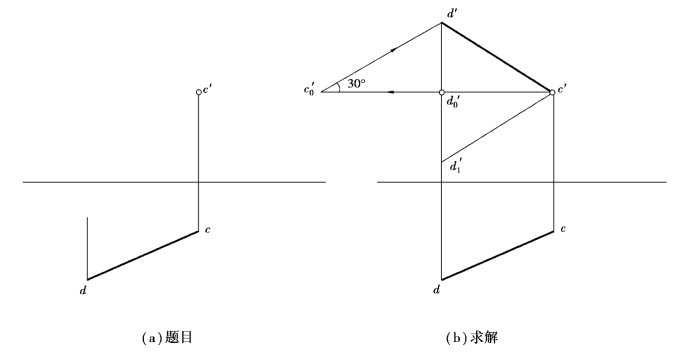
图2.26　已知α=30°，求直线的投影