画法几何与阴影透视：直线上的点

1）直线上的一般点

空间点与直线的关系有两种情况：点属于直线；点不属于直线。当点属于直线时，则有以下投影特性（如图2.16）：

①该点的各投影一定属于这条直线的各同面投影。

②点将直线段分成一定的比例，则该点的各投影将直线段的各同面投影分成相同的比例，这条特性称为定比特性。

一般来说，判断点是否属于直线，只需观察两面投影就可以了。例如图2.17中的直线AB和两点C、D，点C属于直线AB，而点D就不属于直线AB；但对于一些特殊位置直线，则一般应该观察第三面投影才能决定。例如图2.18中的侧平线CD和点E，虽然e在cd上，e′在c′d′上，但当求出它的W面投影e″以后，e″不在c″d″上，所以点E不属于直线CD。也可以通过定比性来判断，如图2.18（b）所示。当然从2.18中也可以看出，显然e′c′∶e′d′≠ec∶ed，则E点不在CD上。

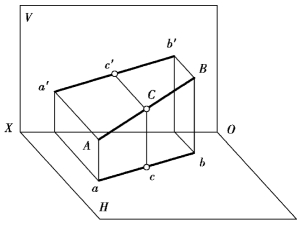
图2.16　属于直线的点

图2.17　C点属于直线，D点不属于直线

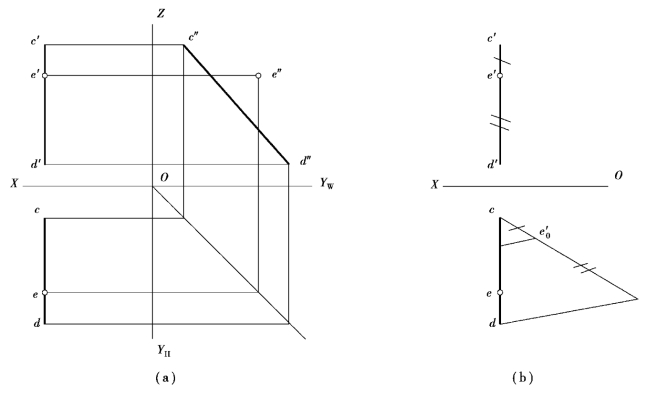
图2.18　特殊位置直线点的从属性判断

【例2.5】在线段AB上求一点C，C点将AB线段分成AC∶CB=3∶4。

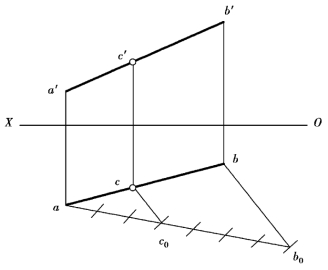
图2.19　点分线段成定比

【解】作图如图2.19所示。

①过投影a作任意方向的辅助线ab0，将之七等分，使ac0∶c0b0=3∶4，得c0、b0。

②连接b、b0，再过c0作辅助线平行于b0b。

③在水平投影ab上得C点的水平投影c，再由c向上作铅垂线，交AB的正面投影a′b′于c′。

【例2.6】已知属于侧平线CD的点E的正面投影e′，请作出E点的水平投影e。

【解】如图2.20所示，本题有两种作法：

①把正面投影e′所分c′d′的比例m∶n移到cd上面作出e，如图2.20（a）所示。(www.xing528.com)

②先作出CD的侧面投影c″d″，再在c″d″上作出e″，最后在cd上找到e，如图2.20（b）所示。

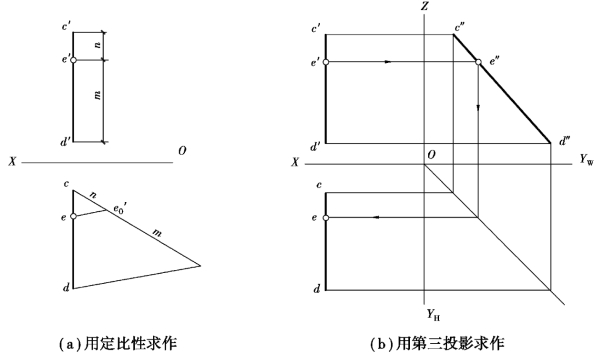
图2.20　侧平线上的点

2）直线上的迹点

直线延长与投影面的交点称为直线的迹点，其中与H面的交点称为水平迹点（常用M表示），与V面的交点称为正面迹点（常用N表示），与W面的交点称为侧面迹点（常用S表示）。

如图2.21所示，给出线段AB，延长AB与H面相交，得水平迹点M；与V面相交，得正面迹点N。因为迹点是直线和投影面的公共点，所以它的投影具有两重性：

①属于投影面的点，则它在该投影面上的投影必与它本身重合，而另一个投影必属于投影轴。

②属于直线的点，则它的各个投影必属于该直线的同面投影。

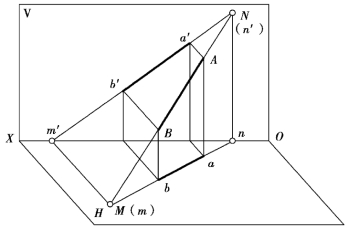
图2.21　直线的迹点

由此可知：正面迹点N的正面投影n′与迹点本身重合，而且落在AB的正面投影a′b′的延长线上；其水平投影n则是AB的水平投影ab与OX轴的交点。同样，水平迹点M的水平投影m与迹点本身重合，且落在AB的水平投影ab的延长线上；其正面投影m′则是AB的正面投影a′b′与OX轴的交点。

这样，就得到在两面投影体系中，根据直线的投影求其迹点的作图方法：

①为求直线的水平迹点，应当延长直线的正面投影与OX轴相交，即得水平迹点M的正面投影m′，再从m′作OX的垂线与直线的水平投影相交，交点就是水平迹点M的水平投影m，M与m重合。

②为求直线的正面迹点，应当延长直线的水平投影与OX轴相交，得正面迹点N的水平投影n，再从n作OX轴的垂线与直线的正面投影相交，交点就是正面迹点N的正面投影n′，N与n′重合。

【例2.7】求作直线AB的水平迹点和正面迹点。

【解】作法如图2.22所示。

①延长a′b′与OX轴相交，得水平迹点的正面投影m′，再从m′向下作OX轴的垂线与ab相交，得水平迹点的水平投影m，此点即为AB的水平迹点M。

②延长ab与OX轴相交，得正面迹点的水平投影n，再从n向上作OX轴的垂线与a′b′相交，得正面迹点的正面投影n′，此点即为AB的正面迹点N。

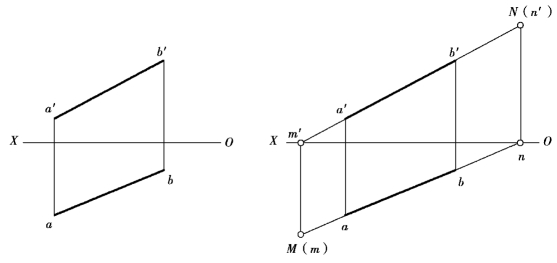
图2.22　直线迹点的求法