如何画出各种位置直线的投影

直线的投影一般仍为直线。因为通过直线上各点向投影面作正投影时，各投射线在空间形成一个平面，该平面与投影面相交于一条直线，这条直线就是该直线的投影。只有当直线平行于投影方向或者说直线与投影面垂直时，其投影则积聚为一点，如图2.14所示。

图2.14　直线投影

图2.15　直线的三面投影

从几何学中我们知道，空间直线的位置可以由属于直线上的两点来决定，即两点决定一条直线。因此，在画法几何学中，直线在某一投影面上的投影由属于直线的任意两点的同面投影来决定。如图2.15所示，当已知属于直线的任意两点A、B的三面投影，连接两点的同面投影，即连接a，b，a′、b′，a″、b″而得到直线AB的三面投影ab、a′b′、a″b″。

直线与投影面的位置有三类：平行、垂直、一般。与投影面平行或者垂直的直线，称为特殊位置直线。

1）投影面的平行线

平行于某一投影面而倾斜于其余两个投影面的直线，称为投影面平行线，投影面平行线的所有点的某一个坐标值相等。其中，平行于水平投影面的直线称为水平线，z坐标相等；平行于正立投影面的直线称为正平线，y坐标相等；平行于侧立投影面的直线称为侧平线，x坐标相等。表2.1列出了这三种直线的三面投影。

表2.1　平行线的三面投影和投影特性

续表

(www.xing528.com)

表中α表示直线对H面的倾角；β表示直线对V面的倾角；γ表示直线对W面的倾角。分析上表，可以归纳出投影面平行线的投影特性：

①直线在它所平行的投影面上的投影反映实长（即有全等性），并且这个投影与投影轴的夹角等于空间直线对相应投影面的倾角；

②其余两个投影都小于实长，并且平行于相应的投影轴。

2）投影面的垂直线

垂直于某一投影面的直线，称为投影面垂直线，投影面垂直线上的所有点有两个坐标值相等。显然，当直线垂直于某一投影面时，必然平行于另两个投影面。其中，垂直于水平投影面的直线称为铅垂线；垂直于正立投影面的直线称为正垂线；垂直于侧立投影面的直线称为侧垂线。表2.2列出了这三种直线的三面投影。

表2.2　垂直线的三面投影和投影特性

续表

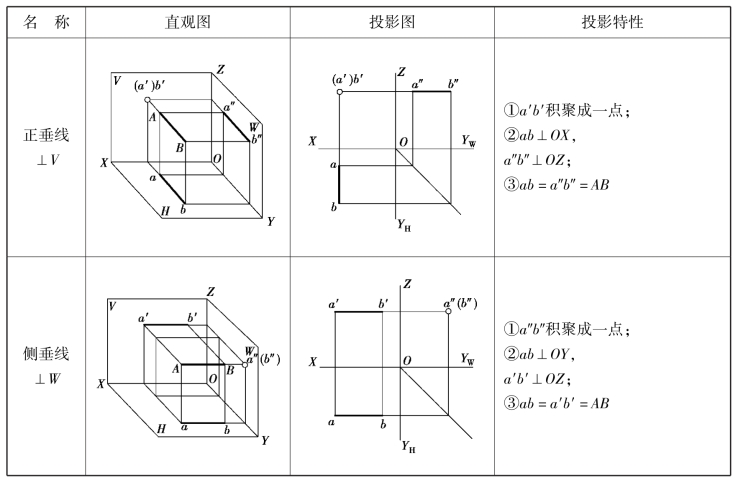
分析上表，可以归纳出投影面垂直线的投影特性如下：

①直线在它所垂直的投影面上的投影成为一点（积聚性）。

②其余两个投影垂直于相应的投影轴，并且反映实长（显实性）。