(1)月均水温距平序列的小波变换。根据宜昌站月均水温距平时间序列 (N=612),采用复Morlet小波进行连续小波变换,可以得到小波变换系数的实部及模,分别绘制其小波变换等值线图,见图4-13 (a)和图4-13 (b)。小波系数实数为正时,表示水温偏高,图中用实线绘制;为负时表示水温偏低,图中用虚线绘制;小波系数为零则对应突变点。
根据图4-13 (a)中可分析出水温存在明显的年际变化和年代变化,从上至下分析得出水温存在16~20年、10~12年、2~6年3类尺度的周期变化规律。从较大尺度16~20年分析,水温经历了低→高→低→高→低→高→低→高8个循环交替,具体表现为1956—1966年、1971—1976、1982—1989年、1994—2003年水温偏低;1967—1970年、1977—1981年、1990—1993年、2003—2006年水温偏高,直到2006年等值线仍为闭合,2006年后一段时间内水温仍偏高。从尺度10~12年分析,水温经历了低→高→低→高→低→高→低→高→低→高→低→高→低→高14个循环交替,其中2006年水温偏高曲线仍未闭合,与16~20年尺度的变化一样,2006年以后一段时间仍将处于水温偏高期。这两个尺度的周期变化在整个分析时段表现稳定,具有全域性。2~6年尺度上,则有更多的循环交替。根据图4-13 (b)可以看出16~20年和10~12年尺度的小波系数的模较大,说明这两个周期变化最明显;其次是2~6年尺度的周期变化。
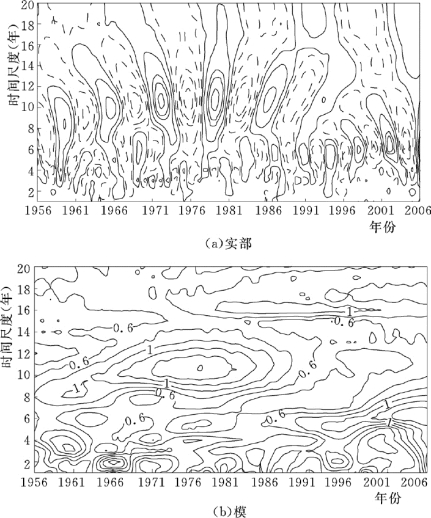
图4-13 月均水温距平序列小波变换等值线图(https://www.xing528.com)
(2)月均水温距平序列的小波方差。利用式(3-11),计算了月均水温距平序列的小波方差,根据计算结果,确定各序列存在的主要周期,小波方差见图4-14。图4-14中有5个峰值,分别对应2年、6年、10年、16年和19年的时间尺度,第一峰值是10年尺度,说明10年左右的周期震荡最强,为月均水温变化的第1周期,第2~5周期依次为16年、19年、6年和2年。
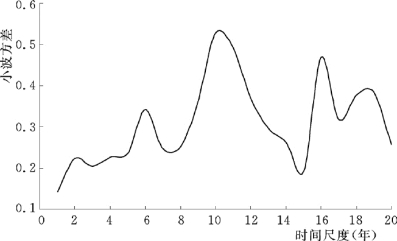
图4-14 月均水温距平序列小波方差
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




