希腊帕特农神庙的神奇比例及金字塔的奥秘

1．帕特农神庙中的神奇比例

再回到古希腊最著名的建筑帕特农神庙（图9－22），它是希腊那些发明了几何学的最优秀的人建造的。因此，它是把神圣的几何运用于建筑之中的一个具有原型意义的范例。我们知道，帕特农神庙的几何结构复杂而周密，建筑设计者伊克提诺斯甚至为此专门写了一本书，可惜此书失传了。很多书籍宣称帕特农神庙的尺寸之美来自于黄金分割率和φ的运用，实际上这不是事实。结合表9－1给出的帕特农神庙的尺寸，我们来作一仔细分析。

帕特农神庙正面的几何结构是非常简单的：神庙的正面是长方形，正面宽度是8根石柱的高度的3倍，正面宽度是正面高度（不包括山形墙）的2．25倍。这与φ的值（1．618）显然相差甚远，但这一数字却是等于比例94。通过下面的分析，我们会发现与φ相比，9这个数字在帕特农神庙中的作用要重要得多。

图9－22 希腊雅典的帕特农神庙

山形墙，希腊人知道得很清楚，是相对独立的，不应该把它作为帕特农神庙（长方形）正面的一部分（把这个三角形的山形墙包含在内所算得的比例没有意义，但不把它包含在内所算得的比例数却有意义）。

这就不奇怪了，这个三角形山形墙的底和高的比例是101．25／（57．60－44．58）＝101．25／13．02＝7．77777…，是个无限循环但引人入胜的数字，它可以用分数表示为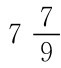，希腊人已经看到了这一点。

表9－1 帕特农神庙的尺寸

注：帕里萨拉是希腊的一种长度单位。

（1）内堂的尺寸

维特鲁威解释说，帕特农神庙外圈的柱廊（或步道）不过是一种拱廊，且围绕着内堂。从本质上来说，柱廊是一个为信徒遮挡地中海频繁暴风骤雨的地方。柱廊的前边（或东端），名为“门廊”（在内殿的前面）。内殿是帕特农神庙的神圣区域，内堂长42．67米，宽21．34米，比例刚好是2∶1（图9－23）。

图9－23 帕特农神庙平面图

（2）柱基尺寸

柱基（平台）是帕特农神庙的地基。从柱基最顶层的台阶开始测量，帕特农神庙宽68．58米、高30．86米，用宽除以高，结果是2．2222…。古希腊人看得出来，这个数就是20／9。

（3）与旧神殿的关系

在波斯人毁了旧神庙之后，建筑师伊克提诺斯戴罪立功，建造了这座神庙，刚好是旧神庙的两倍大也比旧神庙辉煌壮丽。然而，事情不像说起来的那么简单。如果你把旧神庙的尺寸都放大为2倍，你就会发现新神庙的体积是旧神庙的8倍，不符合要求了。和古埃及人一样，古希腊人对建筑物的立方计算（体积计算）也很感兴趣，他们希望新神庙的体积刚好是被毁坏的旧神庙的体积的2倍。

（4）倍立方

如果旧神庙本来的边长为s，那么它的体积为

V＝s3

两倍体积就是

2V＝2×s3

为了得到新神庙的长度n，我们就需要这么计算：

因此，为了把体积扩大为2倍，所有的边都应该乘以系数1．26。

（5）数字9

注意9这个数字，它的比例数总是产生一些匪夷所思的自循环小数，而且小数点后的数字都是同一个数。例如：

这些都是纯位数（纯位数是只包含单一的非零的循环数，如11，22或555555）。确实，用来测量帕特农神庙的两种度量单位——英尺和修正过的希腊尺，互相之间存在着或1．11111…的比例关系。

如果我们采用希腊的另一种长度单位“帕里萨拉”（希罗多德就是用这个单位来描述胡夫金字塔的），我们就得到另一系列的纯位数（表9－2）。

因此，读者可能明白了，帕特农神庙的神圣几何的关键之处是9，而不是φ！

表9－2 神圣几何的关键比值

2．金字塔的神奇比例

提到金字塔，大多数人只想到胡夫金字塔及其周边的金字塔。实际上，胡夫金字塔仅仅是其中最大的一座，在漫长的古埃及历史中，接连出现了不止35座金字塔。(www.xing528.com)

尽管金字塔的外形都差不多，但其斜度、高度和底边长度有所不同，这是因为当初建造者所做的各种尝试和调整。有一座“弯曲金字塔”，甚至在半中腰的地方开始往上改变斜度。现在关于金字塔的高度，有时是估算的，因为有的金字塔的压顶石和外层石头已遗失。因此，计算金字塔的高度和斜度，在几何学上看似简单，其实问题重重。

1．计算赛卡德

古埃及的数学著作《莱因德纸草书》（Rhind Papytus）上，记载了许多基本的数学问题，包括对金字塔的斜度（或称“赛卡德”）的计算。其中有一个问题是这样的：如果一座金字塔的高度是8肘尺，底边是12肘尺，它的“赛卡德”是多少？

金字塔的赛卡德，是它的4个三角形侧面与其水平的底面之间的倾斜度。为解答此问题，使用古埃及长度单位皇家肘尺为基本长度单位：1皇家肘尺＝7掌＝28指。

赛卡德通常是这么表达的：每垂直升高1肘尺，在水平上则有若干掌——用现代几何学的说法表示，就是三角形斜面与底面夹角的余切，但其比值的分子以掌为单位，分母以肘尺为单位。

为了解决《莱因德纸草书》的这个问题，我们需要画出直角三角形FEH。记住距离FE是底边DA的一半，如图9－24所示。

当高度＝8肘尺，底边的一半＝12／2＝6肘尺，用掌来表达＝7×6＝42掌，所以赛卡德掌＝5掌1指。

这个数字就是《莱因德纸草书》提供的那个正确的数字。《莱因德纸草书》的另外3个问题的基础，也是同样的赛卡德比例，这表明赛卡德在金字塔的设计中是非常重要的。

图9－24

（1）赛卡德

古埃及人所做的与金字塔有关的主要计算，是对赛卡德的计算。如果你调查过全部金字塔的赛卡德，你会发现它在一个数值范围之内，从3．5（易普特一世，Iput I）到7．7（赛索斯特里斯二世，Senusret）。但是，有两类明显不同的金字塔赛卡德相同，一种的赛卡德是精确的5．25，另一种的赛卡德是精确的5．5。有意思的是，赛卡德相同的金字塔，在地理上也靠得近。从表9－3可以看出，两种最常用的赛卡德是：

5．25—乌塞尔卡夫、珀辟一世、珀辟二世、哈夫里、特第和伽卡尔的金字塔。

5．50—胡夫、斯奈夫鲁、曼卡雷、尼乌赛尔的金字塔以及吉萨的4座小金字塔。

这两种赛卡德基于简单的整数比值：5．25基于高度与底边的比值2∶3，5．50基于高度与底边的比值7∶11。所有的赛卡德，都基于这种直截了当的整数比值。

表9－3 部分金字塔的尺寸

（2）估计精确的高度

这些赛卡德既不是主观的，也不是一个概算值，因此，它们可以用来计算金字塔的高度（测量赛卡德和底边，比测量高度更容易、更精确）。

根据何来？事实上，为了说明这个问题，我们应考虑一下另外两个几何学知识：一个是1皇家肘尺可分为7掌，一个是π的值。

首先看皇家肘尺的单位划分。1皇家肘尺可分为7×4＝28指，这与月球每月运行轨道上的28个区域是对应的。然而，因为7是素数，也是一个有魔力的数，因此，把它设为长度是很奇怪的，因为它不能被任何其他整数整除。在其他度量体系当中，长度通常可以被2，4，8，10或12之类的数整除。这样一来，可以比较容易地将东西分成2或3份。但是，古埃及人的皇家肘尺却不能进行这种简单的分法。

2．金字塔尺寸与圆和7／11的关系

据说胡夫金字塔的底边周长，正好等于以此金字塔的高度为半径的圆的周长。我们以肘尺为单位，来验证一下：

底面周长＝4×440＝1760

圆周长

计算圆的周长和面积，就不得不与3．14159…这个无限循环小数纠缠，我们用π来表示它。但是，我们也可以用简单的整数来表示它因此，圆的面积＝π×半圆的周长

因此，半径为7肘尺的圆的周长等于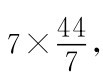即44肘尺。这也意味着半径为1肘尺的圆的周长是44掌。因此，计算半径为任何肘尺的圆的周长就变得容易了。比方说，半径是3肘尺，则周长为掌。这些都是干净利索的整数，没有令人恼恨的无限小数。

现在，你该明白了为什么古埃及人把他们的肘尺分为7个单位了，这是为了把关于圆的计算简单化。基于以上两点，关于埃及的许多金字塔为什么采取5．5作为赛卡德或者斜度，也就明显了。因为这个斜度意味着金字塔的高度与底边的比值为7∶11，而7∶11已经包含了π的数元素（7和22），因此金字塔的底面正方形、侧面三角形和圆形（完美图形）之间，就有了直接的关系。7和11，也出现在胡夫金字塔的其他方面，比方说，胡夫金字塔“大甬道”的两边各有7根枕梁互相制衡。

3．胡夫金字塔对φ的运用

我们再来看看说明赛卡德的计算的那张示意图（图9－24），注意垂直的三角形HEF，它们是沿着胡夫金字塔的一个侧面的正中间往里切到一半形成的。现在，我们将以肘尺为单位，来计算这个所谓的“胡夫金字塔三角形”。它的高HE是280，底边FE是220（即胡夫金字塔底边长440肘尺的一半）。把这两个尺寸都除以220，就可把这个三角形的底边FE简化为1，结果是（2727是无限循环节）＝因此，斜边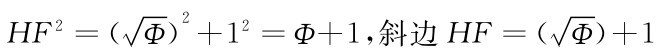（把两条边开方）＝Φ（Φ的一个特例）。因此，如果你考虑到φ与生长之间存在着特别的关系，那么，与跟死亡和来世的关系相比，胡夫金字塔或许更多地与生育、生长有关。