数学文化选粹：和谐与美的重要意义

“数学是一个有机的统一体，它是生命存续的一个必要条件，是所有各部分不可分离的结合”（希尔伯特语）。庞加莱在《科学的价值》一书中强调“内部和谐是唯一的美”“普遍和谐是众美之源”。和谐是一种“度”，一种中庸的最佳状态。数学的统一美正是表现在各种数学关系结构的协调一致上，各种数学方法的联系沟通和它的各部分之间及部分与整体之间的高度和谐与统一。它是客观世界同一性在人们认识中的反映，并由此带给人愉悦的心理感受。

和谐寓于统一之中，和谐和统一是数学美的最高境界。

科学中关于用数学的和谐与统一来进行的工作有许多著名的例子。除了牛顿的工作，爱因斯坦的狭义与广义相对论的研究也是统一性的一种追求。徐利治、郑毓信在他们的著作《数学模式论》中就曾举过门捷列夫关于元素周期表对化学元素和谐统一性质的研究所起到的巨大作用。他们写道：“门捷列夫在表中留下了不少的空位，而这主要就是出于和谐性的考虑，因为，不然的话，在整体上就不可能体现出明显的周期性。门捷列夫在当时依据周期性预言了与空位相对应的化学元素的存在及其主要的性质。这些预言后来都得到了证实。例如，门捷列夫预言在铝与铟之间的空位是未知元素亚铝的位置，它的原子量是68，比重是5．9～6。1857年，法国的勒科克·布瓦保德朗在比利牛斯锌矿发现了镓（Ga），计算出其比重为4．7。门捷列夫就写信指出应当是5．96，后者起初不信，但后经反复计算发现果然是5．96。”这一例子再次表明了和谐与统一的美学思想在科学研究中所具有的重要意义。

在数学史上，代数与几何曾长期分离，而解析几何的诞生却是一次数学上的统一过程。运用解析几何的方法，平面、空间上的点被表示为一个二元或三元数对（x，y）或（x，y，z），几何中的直线与曲线、曲面被表示为代数方程，而代数中的矩阵、行列式在几何研究中也起到重要作用。它把几何图形的某些内在联系揭示得更清楚，从而也使得人们更容易看清它们之间的和谐与统一，这就是代数与几何和谐与统一的进一步表现。

例7－1 平面上过点（x1，y1）和（x2，y2）的直线方程是

而平面上过不共线的3点（x1，y1），（x2，y2）和（x3，y3）的圆方程是

平面上过一点（x1，y1），（x2，y2），（x3，y3），（x4，y4）和（x5，y5）的圆锥曲线方程是(www.xing528.com)

一个式子是另一个式子的推广，形式整齐、和谐而美观，而且使我们非常容易记忆。进一步地，由此我们即可写出3点（x1，y1），（x2，y2），（x3，y3）共线的条件是

同时，我们又可立即写出3直线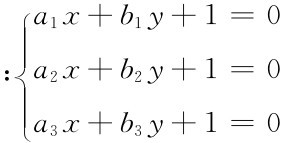

共点的条件是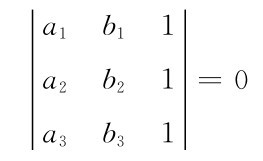

多么的对称、和谐、整齐与美观呀！

例7－2 关于数学的和谐美我们再看一个非常美妙的公式eiπ＋1＝0。这里，包含了整数0，1，包含了自然对数的底e，包含了圆周率π，还包含了虚单位i。0是加法的单位，1是乘法的单位，如果把公式改变一下就成为eiπ＝－1，又包含了负数－1。毕达哥拉斯学派以整数与整数的比作为世界的根本，一直不容许有无理数的产生，我们前面也曾说过负数是多么的令人难以接受，更不要说虚数了，而圆周率π的研究曾是数千年数学家梦里萦怀的东西。而这6个数却统一在这样一个简单的公式里，这还不美吗？

数学中关于统一与和谐美的更著名的工作还有著名的法国的布尔巴基数学学派，曾用结构的观点来统一数学。他们认为数学有3种基本结构：代数结构、顺序结构和拓扑结构，所有的数学无非是这些结构及其不同的组合。虽然布尔巴基学派的工作还有许多缺憾，但他们的工作却进一步揭示了数学自身的和谐、统一及其美的内容。