近世代数发展简史及多项式理论的重要成果

代数学的另一个重要内容——多项式理论是由高次方程求根问题发展起来的。和一次方程组的情形不同，一元高次方程的求解要困难得多，人们着眼于寻求高次方程的代数解法。所谓代数解法就是和一元二次方程一样，希望由方程的系数通过加、减、乘、除、乘方、开方这6种运算把根表示出来。这件事情前后大约经历了300多年。1515年，意大利数学家菲洛解决了缺二次项的三次方程的求解问题，但他的解法并未发表，只是告诉了他的一个学生。1535年（菲洛逝世后约10年），该学生以上述这类方程求解问题向意大利数学家塔尔塔里亚（N．Tartaglia，1500—1557）挑战，后者应战，仅用8天时间解决了这类问题，并当众显示结果，但未给出推导过程。数学物理学家卡丹得知，要求塔尔塔里亚把解题秘诀告诉他，并发誓按制度办事绝对保密。在这种情况下，塔尔塔里亚才将解法告诉了卡丹。卡丹于1545年发表《大法》一书，塔尔塔里亚发现自己的秘诀被泄漏无遗，遂向卡丹发难，并于次年发表了自己的解法。卡丹的学生弗尔拉里发表文章为老师辩护。这场论战，使三次方程的求解过程广为流传。现在的求解公式，仍称为卡丹公式。

考虑一元三次方程

y3＋ay2＋by＋c＝0

令

则得

x3＋px＋q＝0

其中

再令

x＝u＋v

得

u3＋v3＋q＋（3uv＋p）（u＋v）＝0

选u，v使

3uv＋p＝0

于是，有

u3＋v3＋q＝0

再加上方程

韦达定理说明，u3，v3是方程

的根，即

由u，v可得原方程的根。

1540年，弗尔拉里发现了4次方程的代数解法。

1629年荷兰数学家吉拉尔在《代数新发现》中提出n次多项式方程有n个根，但是没有给出证明。1637年笛卡儿（1596—1650）在他的《几何学》的第三卷中提出：一个多少次的方程便有多少个根，包括他不承认的虚根与负根。18世纪，对方程根的存在性这个问题引起数学家们的议论。

1742欧拉提出，任意次数的实系数多项式都能够分解成一次和二次因式的乘积，他还指出之所以不能都分解成一次因式，是因为复根共轭成对。法国数学家达朗贝尔（R．D′Alembert，1717—1783）于1746年首先给出“代数学基本定理”。这个定理断言：“每个实系数或复系数的n次代数方程至少有一个实根或复根。”因此，r次代数方程有r个根。达朗贝尔、拉格朗日和欧拉都曾试过证明此定理，可惜所有这些证明都预先假设多项式的一些“理想的”根确实存在，然后去证明在这些根中至少有一个是复数，这样的证明并不完全。1770年，法国数学家拉格朗日（Lagrange，1736—1813）从研究二、三、四次方程求解的规律入手，引入了排列与置换的概念，写出了《关于代数方程解法的思考》的文章，指出高于四次的代数方程可能没有代数解法，但没有给出证明。1799年，22岁的高斯在其博士学位论文中给出这个定理第一个严格的证明，还附带证明了：任一r次实系数多项式必能分解成一次或者二次实系数因式的乘积。高斯的这一证明开创了数学中证明存在性的一种新的方法。后来他又给出另外3个证明，时间分别是在1814—1815年、1816年和1848—1850年，所以，有些学者也认为代数基本定理是高斯提出的。20世纪以前，代数学所研究的对象都是建立在实数域或复数域上的，因此代数基本定理在当时曾起到核心的作用。

1824年，挪威数学家阿贝尔（Abel，1802—1829）证明了高于四次的一般形式的代数方程没有代数解法。至此，人们在长达300多年内寻求高于四次方程的根的公式失败的原因终于有了理论依据。

为什么四次及四次以下的代数方程有代数解法，而高于四次的方程就没有代数解法呢？这个问题吸引了法国青年数学家伽罗瓦（Galois，1811—1832）。1829年，年仅18岁且仍是巴黎高等师范学院一年级学生的伽罗瓦在熟读了拉格朗日和阿贝尔的论文后，深受启发，他想寻找一种统一的方法讨论能否用根式求解高次方程，即在一般的理论框架下研究这个问题。对于已知的方程，伽罗瓦考虑它的根的置换构成的某个方程根的内在特征，即这些性质对方程是否存在代数解法取决定性作用。于是便开始对这个置换集进行独立的研究。这个置换集后来被称为伽罗瓦群。他证明了一个代数方程如果可用根式求解，则相应的伽罗瓦群是一个可解群。作为这个结果的一个推论是：对应于一般形式的n次代数方程的伽罗瓦群，只有当n＝1，2，3，4时才是可解群。伽罗瓦把这些成果写成了论文《关于代数方程论的研究报告》，于1829—1830年先后两次把《报告》呈交法国科学院，但都被遗失。他再重写，定名为《关于根式求解方程之条件的研究报告》，第三次呈交科学院，被审稿的院士否定了。后来他将其写成一本仅有60页的著作，却无法出版。大约过了15年，才有很少的人重新注意他的工作，克服了很大的困难才弄明白，大约在他逝世后40年即1870年，他的成果才被世界公认，后人称其为伽罗瓦理论。(www.xing528.com)

这里特别要指出的是，伽罗瓦群的所有重要性质，如可解性等，实际上不依赖于被置换对象的固有特征，从而产生了“抽象性”的概念，开创了代数学领域里的一个崭新的分支——群论，这是研究“代数体系”的开端。什么是“代数体系”呢？简单地说，就是带有运算的集合。人们在研究数的运算时，发现这些运算遵循一些规律，例如交换律、结合律、分配律等。数学家们把具有某些运算并满足一定规律的集合（不一定是数集），赋予一些特殊的名称，如“群”“环”“域”等，从而构成了不同的代数体系，以下以整数集合、有理数集合为例说明这些概念。

以I表示由整数所组成的集合。在I上有加法运算“＋”，并且I在这个运算下满足：

1）I对加法运算是封闭的，即若a、b∈I，则a＋b∈I。

2）结合律成立，即若a，b∈I，则a＋b∈I，a、b、c∈I，则a＋（b＋c）＝（a＋b）＋c∈I。

3）对a、b∈I，则方程a＋x＝b及y＋a＝b在I内有解。

这时我们就说I在加法运算下构成一个群（Group）。一般来说，如G是一个非空的集合，且在G上有一个代数运算（通常称为乘法），若G在这个运算上满足上述性质1）、2）及3），则G称为是一个群。

对于I中的元素，a、b还有

4）a＋b＝b＋a，所以I对加法构成一个交换群。

除了加法外，I上还有另一个运算，即乘法运算“×”，且满足：

5）I对乘法运算也是封闭的，即若a、b∈I，则a×b∈I。

6）乘法结合律成立，即若a、b、c∈I，则

a×（b×c）＝（a×b）×c∈I

7）加法与乘法的分配律成立，即若a、b、c∈I，则

a×（b＋c）＝a×b＋a×c （b＋c）×a＝b×a＋c×a

即对加法构成一个交换群，又对乘法封闭且满足乘法结合律及分配律，即满足性质5）、6）、7），我们称I构成一个环（Ring）。一般来说，若G是一个集合，在G上有两种代数运算，对其中一种称为加法的运算，G构成一个可交换群；对另一种称为乘法的运算，满足性质5）、6）、7），则G称为一个环。

如果G是一个环，并且对a、b∈G，则有ab＝ba（这里ab表示对a、b作乘法运算，略去了符号“×”），则G称为交换环。一个交换环G称为一个域（Field），如果G还满足：

8）G中至少包含一个不等于零的元。

9）对乘法运算，G中有一个单位元，即存在e∈G，使对任意a∈G有ea＝ae＝a。

10）G中每个不等于零的元对乘法运算有一个逆元，即若a∈G，且a≠0，则存在a－1∈G，使得aa－1＝a－1a＝e。

按照上面的定义，上述全体整数的集合I满足性质8）与9），其中对乘法运算的单位元就是普通的数“1”。但是a∈I，a≠0，共逆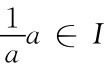（注意：全体整数集合I，对加法运算来说，它的单位元是“0”，a的逆元是－a），即A在I内无对乘法运算的逆，故条件10）不成立，所以I不是域。同样，全体实数的集合和全体复数的集合都是域。研究群、环和域等代数体系的代数学分支，称为抽象代数学或近世代数学。

以正整数为研究对象，但不是从运算的观点，而是从数的结构的观点来研究，即从一个数可用其他性质较简单的数来表达的观点研究数的代数学分支，称为数论。数论又分为初等数论（其内容基本上不借助于其他数学分支的方法）、代数数论（研究整系数多项式的根——代数数）、几何数论（研究直角坐标系中坐标均为整数的全部“整点”——空间格网）、解析数论（用分析方法研究素数的分布）。初等数论和几何数论产生于17世纪中叶，解析数论产生于19世纪后半期。

中国数学家在数论方面做出过重要贡献。如4世纪孙子的“求一术”，13世纪秦九韶的“大衍求一术”，是同余式理论的完整结果。近代的华罗庚、陈景润等在解析数论方面都做出过突出的贡献。

代数学领域内还包含了一些新兴的学科，例如代数几何、代数拓扑、拓扑群、布尔代数等。我们将在第八章中以布尔代数在搜索引擎的索引中的应用为例介绍代数学的新发展。