微积分的发展史及争论：牛顿与莱布尼茨的遗憾

1．18世纪微积分的发展

牛顿与莱布尼茨的微积分都存在着不足，从17世纪末开始以及整个18世纪，在西欧各国的科学界、思想界展开了一场规模宏大的激烈争论。在英国，牛顿及其维护者们同英国天主教的大主教贝克莱为微积分的真理性展开了一场争论；在欧洲大陆，以莱布尼茨为中心的大陆派与法国科学院院士洛尔以及荷兰物理学家、数学家尼文太关于微积分展开了一场大辩论，他们都是抓住微积分赖以建立的基础——无穷小大肆攻击，声称应立刻把微积分从数学中“剪裁掉”。另一场大争论是在英国派与大陆派之间进行的，他们是为关于建立微积分的优先权问题。牛顿的支持者是著名数学家泰勒与麦克劳林；莱布尼茨的维护者则是著名的数学家伯努利兄弟。争论把欧洲科学家分成势不两立的两派，其结果是英国和欧洲大陆的科学家停止了思想交换。其实他们彼此独立地发现了微积分。当然牛顿发现在先，而莱布尼茨则发表得早。莱布尼茨没有像牛顿那样对数学研究得更深，但他的知识较广，并且作为一名分析学家和数学物理学家虽不及牛顿，但他也许对于数学形式有比较敏锐的想象力和卓越的本能。因为牛顿在微积分方面的主要工作和在《原理》中使用了几何方法，所以在他逝世后差不多100年中，英国人继续以几何为主要工具；而欧洲大陆则接受了莱布尼茨优越的符号之后，加以发扬光大，很快获得了丰硕的成果。

克莱、瓦里斯、巴罗，他们之后有巴罗的学生牛顿、科林斯、格里高利，牛顿的追随者有泰勒（Brook Taylor，1685—1731）、麦克劳林（1698—1764）、托马斯·辛普生、约翰·兰登（英国皇家学会会员，《残差分析》对导数定义提出了代表性的方案之一——代数的微分学）。

在欧洲大陆，以莱布尼茨为中心的大陆派继承并光大了原有的工作。其代表人物有被誉为法国3巨头的罗伯瓦尔、费马、帕斯卡，更有在帕斯卡的好友惠更斯影响下成长起来的莱布尼茨、洛尔、莱布尼茨的朋友伯努利兄弟（雅各布·伯努利和约翰·伯努利），之后还有约翰·伯努利的两个儿子（尼古拉和丹尼尔）和学生（欧拉和洛必达），以及在他们的影响下成长起来的达朗贝尔和被誉为“3L”的拉普拉斯、拉格朗日（欧拉的学生）和勒让德，他们的继承人有傅里叶和泊松。由于这些数学家的努力，产生了常微分方程、偏微分方程和级数论等。

2．19世纪微积分现代形式的确立

19世纪初叶，由于在微积分发展的初期还没来得及夯实其理论基础，因此常遭到种种非议，其中最为著名的当属贝克莱悖论和格兰弟悖论。数学家们开始了微积分理论基础的重建与严格化等奠基工作。

（1）贝克莱悖论

现在的微积分可谓至善至美。但在牛顿和莱布尼茨创立微积分学的初期，由于当时微积分学的理论基础非常薄弱，常常有不能自圆其说的情况。因此，它遭遇到了当时不少人的猛烈抨击，如贝克莱（Gearge Berkeley，1685—1753）、尼文太等。尤其是贝克莱大教主，他精通数学，为了维护宗教利益，他挑出了当时牛顿、莱布尼兹理论中一些不严格的地方大肆攻击，比如，1734年撰写了《分析学者——致不信神的数学家》一书。书中他批评道：牛顿在求瞬时速度的过程中，若Δs＝t2，在t＝2时，求v2。

Δs＝（2＋Δt）2－22＝4Δt＋（Δt）2，

这时牛顿令Δt＝0，并认为v2＝4。这样的推导是很成问题的，因为在数学上总是非零数作除数，所以作为除数的Δt不能等于零；可是牛顿最后又采取割尾巴的方法，又令Δt＝0。这样Δt一会儿是零，一会儿又不是零，这不是自相矛盾吗？既然代表时间它就应该是一个数量，这个虚无缥缈、漂泊不定的数量Δt，不正是我们教会里面所说的鬼魂吗？不过他不是消失了肉体的人的鬼魂，而是消失了数量的鬼魂，并指出这是“依靠双重的错误得到了虽然不科学却是正确的结果”“每门科学，人们是用原理证明结论，而不是用结论来证明原理”。

贝克莱对莱布尼兹同样进行了无情的攻击，他说：“莱布尼兹及其追随者，在进行微积分运算时，竟从不脸红地首先承认然后舍弃无穷小量，稍具思考能力的人，在理解时仔细一点，在推理时公正一点，就不会接受这些。”

数学家们把上面的问题称为“贝克莱悖论”。不可否认，贝克莱一针见血地指出了问题的要害。虽有不少文章对其进行反驳，但由于他们未抓住问题的症结，也未对微积分的逻辑缺陷和理论建构采取任何补救措施，反驳显得软弱无力，倒是贝克莱一时占了上风。史学家们把此称为数学史上的第二次危机。

对于这个问题，我们现在知道它是一个无穷小量，而不是一个具体的数，只是一个以零为极限的变量。马克思曾经做过研究（可参见他的《数学手稿》），得出与此相吻合的结论：无穷小量实质上不过是变量（无穷小量）在矛盾运动中的“是零”与“非零”的对立统一关系，而微分是“扬弃了的差”，可概括为否定之否定的过程（既表明状态又表明过程），这就给微积分进一步的发展提供了哲学依据。

其实这个问题的彻底解决是在极限论建立之后。

（2）格兰弟悖论

在这一时期还有一个叫格兰弟（Grandi）的意大利修道士，他是比萨大学哲学和数学教授，以对玫瑰线的研究而著名。他就级数的收敛、发散含混不清的问题，提出了“从虚无创造万有”的悖论。他举出了一个无穷级数x＝1－1＋1－1＋…求和的例子。

因为

所以(www.xing528.com)

x＝0

又

所以

x＝1

综上立得：0＝1，在等式两端乘上任何数，就得到0＝任何数，所以格兰弟说“从虚无（0）创造万有（任何数）”。

其实，由数学分析中的级数重排理论（即无穷和式先后次序不满足加法交换律），可以重新排的级数至少得收敛（条件收敛或绝对收敛）。显然上述级数通项不满足这一条件，故不收敛。

学过实变函数论或者了解级数的进一步发展的人都知道，微积分里的级数求和法是柯西提出的，是以部分和的极限作为无穷级数的和。一般地，若L是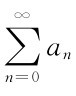的柯西和，即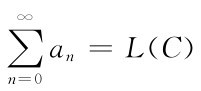；而利用阿贝尔（Abel）定理可推广柯西求和法：设有无穷级数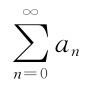，如果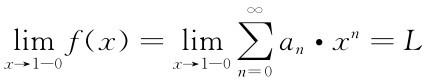存在且有限，则称L为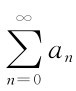的阿贝尔和，记为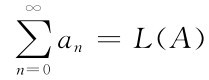（可以证明：如果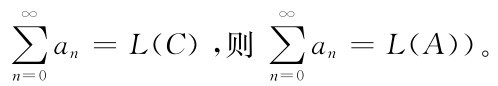但有一些无穷级数，它的柯西和不存在。例如，1－1＋1－1＋…＋（－1）n－1＋…按柯西意义下的和不存在，但按阿贝尔意义其和存在且为1／2。它的实际意义何在，这里倒是有一个有趣的解释：

一位父亲在临终前将一块宝石传给他的两个儿子，他规定两个人轮流保存这块宝石，这样比较公平。我们假定每个儿子都是长生不老的，每人保存期是一年，这样对每一个儿子来说，一得一失，依此往返，得就是＋1，失就是－1，用级数来表示为1－1＋1－1＋…＋（－1）n－1＋…，由阿贝尔和可知为1／2，这恰是每一个儿子对这块宝石的所有权。

上述列举的两个例子都反映了有限和无限、零与非零的矛盾，它们说明了微积分学的不严格，是第二次数学危机的主要导火线。

17世纪中叶，微积分建立以后，分析学飞快地向前发展，18世纪达到了空前灿烂的程度，其内容的丰富，使人来不及检查和巩固这一领域的理论基础，因而遭受到种种非难。19世纪初，许多迫切的问题已基本上得到解决，数学家便开始了基础的重建与严格化。

以下从函数概念的发展、极限理论的完成和实数理论的建立这3个方面介绍如下。

1）函数概念的发展。首先由傅里叶、柯西等冲破函数的解析式。柯西在1821—1823年出版的《分析教程》和《无穷小计算讲义》是数学史上划时代的著作。书中给出了微积分的一系列基本概念的精确定义。他给出了精确的极限定义，然后用极限定义连续性、导数、微分、定积分和无穷级数的收敛性，将微积分建立在极限理论的基础上。柯西的工作在一定程度上澄清了在微积分基础问题上长期存在的混乱，向分析的全面严格化迈出了关键的一步。之后狄利克雷、罗巴切夫斯基用对应观点给函数下了定义，最后由黎曼给出了今天的形式。

2）极限理论的完成。是波尔查诺开始将严格的论证引入到数学分析之中。1850年他出版了《无穷的悖论》，堪称是微积分极限理论奠基的先驱。而柯西的工作才使它基本完成，之后，由狄利克雷、黎曼等的贡献，经过魏尔斯特拉斯（Weiertrass）的工作彻底完成了极限理论，魏尔斯特拉斯引进了精确的“ε－N”“ε－δ”等一系列数学语言，给出了实数与极限的准确描述。特别是他引进了一致收敛的概念，消除了以往微积分中不断出现的各种异议和混乱。魏尔斯特拉斯所倡导的“分析算术化”纲领，使他获得了“现代分析之父”的称号。这样，微积分所有的基本概念，都可通过实数和它们的基本运算关系精确地表述出来，由此便建立起了分析基础的逻辑顺序是：实数系—极限论—微积分。由此可以说，极限概念的历史是从动态化过渡到静态化的历史。

3）实数理论的建立。柯西用极限概念为微积分奠定了基础，在这个基础上魏尔斯特拉斯又进一步将其算术化，但这并不等于微积分基础研究已终结，人们愈来愈觉得建立实数连续系统的必要性和迫切性。代德金的实数理论是它的现代形式，波尔查诺的工作是它的先驱，摩托尔的贡献是将微积分建立在集合论上，从而给了微积分一个更坚实的基础。由于摩托尔在1874年所创立的《集合论》，他的关于无穷集的理论可以说是微积分理论的高潮。

3．20世纪微积分的新发展

19世纪末，分析的严格化迫使许多数学家认真考虑所谓的“病态函数”，特别是不连续函数和不可微函数，并研究如何把积分的概念推广到更广泛的函数类上去。1902年，法国数学家勒贝格（Lebesgue，1875—1941）以集合论的“测度”概念建立了“勒贝格积分”，使一些原先在黎曼意义下不可积的函数按勒贝格的意义变得可积，并在此基础上进一步推广了微积分的许多基本概念，重建了微积分的基本定理，形成了一门新的数学分支——实变函数论。这就使得微积分的适用范围大大扩展，引起数学分析的深刻变化。作为其分水岭，人们往往把勒贝格以前的分析学称为经典分析，而把由勒贝格积分引出的以实变函数论为基础而开拓出来的分析学称为现代分析。进一步地，20世纪初由意大利数学家和法国数学家阿达玛、弗雷歇等人在变分法的研究中给出了泛函分析的一些基本概念，并将普通的微积分演算推广到函数空间方面。而抽象空间理论与泛函分析在20世纪上半叶的巨大发展则是由波兰数学家巴拿赫推进的，他提出了比希尔伯特空间更一般的赋范空间——巴拿赫空间，极大地拓广了泛函分析的疆域。泛函分析有力地推动了其他分析分支的发展，使得整个分析领域的面貌发生了巨大变化。泛函分析的观点与方法还广泛地渗透到了其他科学和技术领域。

这里还要提到，1966年鲁宾逊（Robinson）为无穷小概念提供逻辑基础时又提出了非标准分析，微积分还在不停地向前发展着。