牛顿与莱布尼兹：微积分的诞生与争议

17世纪后半叶，英国的牛顿和德国的莱布尼茨以其卓越的天才首先明确地认识到求积问题和作切线问题之间的互逆关系，建立了微积分基本定理，并且系统地总结出一套强有力的无穷小算法，也正是因为这几点，使得他们成为微积分的创立人。

1．牛顿的工作

1642年，艾萨克·牛顿（Isaac Newton，1642—1727）出生在英国一个偏僻小村庄的农场里。1661年6月，牛顿以“减费生”的身份考入剑桥大学三一学院。牛顿从小就有一个好习惯，就是爱动手做一些小机械之类的玩意。入学后，他遇到了恩师巴罗。在巴罗的悉心栽培下，牛顿的学业进步很大。1665年，英国发生了一场大瘟疫，学校放了假，牛顿又回到了老家，他开始了科学研究。

在故乡的3年间，牛顿发现了万有引力定律并做了证明；通过分解太阳光，揭开了光颜色的秘密；创立了微积分。如果当时牛顿向世界公布其中的任何一项，他立即会赢得巨大的荣誉，但是牛顿却对此闭口不谈。

根据他的自述，从1664年他开始研究有关微积分的问题，并于1665年夏至1667年春在家乡躲避瘟疫期间取得突破性进展。从1665年开始到1691年，牛顿对微积分的创造性成果主要有：

1665年1月，建立“正流数术”，讨论了微分方法。

1665年5月，建立“反流数术”，讨论了积分方法；10月将其研究成果写成“流数简论”，虽未发表，但已在同事间传阅，这是历史上第一篇系统的微积分文献。

1669年，写成《运用无穷多项方程的分析学》（简称《分析学》，由此后人称以微积分为主要内容的相关学科为“数学分析”）。

1671年，写成《流数法与无穷级数》（简称《流数法》）。

1687年，写成《自然哲学的数学原理》（简称《原理》）。这本巨著使牛顿成为当之无愧的数学领袖。

1691年，写成《曲线求积术》（简称《求积术》）。

牛顿把那些“无限增加的量”称为“流量”，用字母x，y，z等来表示；把方程中“已知确定的量”用字母a，b，c等来表示；把每个流量由于产生运动而获得增加的速度，称为“流数”（或直接称之为速度），用带点的字母˙x，˙y，˙z等来表示。

牛顿在“流数简论”中提出了以下两类微积分基本问题：

1）已知各流数间的关系，试确定流数之比。(www.xing528.com)

2）已知一个包含一些流量的流数的方程，试求这些流量间的关系。

显然这是两个互逆的问题。限于篇幅，我们不再详细说明牛顿的流数术。

当伦敦地区的鼠疫结束后，为了获得硕士学位，牛顿又回到了剑桥大学，随后成了一名研究生。27岁那年，他的导师巴罗意识到牛顿至少是一位在数学方面认真研究、有潜力的学者，于是决定辞去他的教授职位，让位于牛顿。牛顿成了教授，但他在教学方面却没有像在科研方面那样取得成功，有时甚至没有一个学生去听他的课。他提出的许多独到的见解甚至没有引起人们的注意，更不要说得到人们的赞誉了。

1672年，他发表了关于太阳光组成的论文，附带谈了一些自然哲学方面的工作。论文却受到了严厉批评，有的科学家甚至对他全盘否定，腼腆的牛顿对此感到沮丧和气愤，并决定以后再也不发表任何论文了。1684年12月，他在数学家与天文学家哈雷的鼓励下又改变了自己的决定，发表了关于彗星轨迹的研究论文。但这一次，他又卷入了关于微积分发明权的争论之中。这使得他再一次发誓，决心将自己的研究秘而不宣。要不是因为哈雷的劝说和财力上的鼎力支持，集牛顿研究成果之大成的《自然哲学的数学原理》（Mathematical Principles of Natural Philosophy，1687）将永远不会公布于世。这部著作问世后，牛顿终于得到了人们的普遍赞誉。《原理》一书一版再版，到1789年为止，英文出了40版，法文出了17版，拉丁文出了11版，德文出了3版。因此也使得牛顿声名显赫，只有当代的爱因斯坦才可以与他媲美。

牛顿一生关于微积分的主要著作有3部：《运用无穷多项方程的分析学》《流数法和无穷级数》和《曲线求积术》。牛顿主要是从运动学的角度来研究和建立微积分的。牛顿在《自然哲学的数学原理》一书中，运用他创立的微积分这一锐利的数学工具建立了经典力学完整而严密的体系，把天体力学和地面上的力学统一起来，实现了物理学史上第一次大的综合。因而《自然哲学的数学原理》是科学史上最有影响、享誉最高的著作之一，在爱因斯坦相对论出现之前，这部著作是整个物理学和天文学的基础。

2．莱布尼兹的工作

莱布尼兹（Gottfried Wilhelm Leibniz，1646—1716），德国最重要的自然科学家、数学家、物理学家、历史学家和哲学家，和牛顿同为微积分的创始人。1661年，15岁的莱布尼兹进入莱比锡大学学习法律；1663年5月，他以《论个体原则方面的形而上学争论》一文获学士学位。在这期间莱布尼兹还广泛阅读了培根、开普勒、伽利略等人的著作，并对他们的著述进行深入的思考和评价。在学习了欧几里得的《几何原本》课程后，莱布尼兹对数学产生了浓厚的兴趣。1664年1月，莱布尼兹完成了论文《论法学之艰难》，获哲学硕士学位。l665莱布尼兹向莱比锡大学提交了博士论文《论身份》。1666年，审查委员会以他太年轻（年仅20岁）而拒绝授予他法学博士学位。他对此很气愤，于是离开莱比锡，前往纽伦堡附近的阿尔特多夫大学，并立即向学校提交了早已准备好的那篇博士论文。1667年2月，阿尔特多夫大学授予他法学博士学位，还聘请他为法学教授。

1667年，莱布尼兹发表了他的第一篇数学论文《论组合的艺术》。这是一篇关于数理逻辑的文章，其基本思想是把理论的真理性论证归结于一种计算的结果。这篇论文虽不够成熟，但却闪耀着创新的智慧和数学的才华，后来的一系列工作使他成为数理逻辑的创始人。

与牛顿的切入点不同，莱布尼兹创立微积分首先是出于对几何问题的思考，尤其是特征三角形的研究。1684年10月，莱布尼兹在《教师学报》上发表了一篇《一种求极大值与极小值和切线的新方法，它也适用于分式和无理量，以及这种新方法的奇妙类型的计算》的文章，这是最早的微分学文献。文中对微分学的基本内容作了初步的阐述，它包含了微分记号以及函数和、差、积、商、乘幂与方根的微分法则，还包含了微分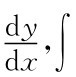等，它们一直使用至今。法在求极值、拐点以及光学等方面的应用。1686年，莱布尼兹又发表了他的第一篇积分学论文《深奥的几何与不可分量及无限的分析》，这篇论文初步论述了积分或求积问题与微分或切线问题的互逆关系，谈到了变量替换法、分部积分法、利用部分分式求有理数的积分等，并给出了摆线方程。莱布尼兹还设计了一套微积分的符号，如dx，dy，

莱布尼兹的一些结果其实是下面这些我们熟知的结论的基础：一阶微分的形式不变性、复合函数求导的链式法则、不定积分的换元法。1677年，莱布尼兹在他的手稿中表述了微积分基本定理：

并明确指出积分表示曲线以f（x）在x∈［a，b］之间的面积。

牛顿在1687年出版的《自然哲学的数学原理》的第1版和第2版中写道：“10年前在我和最杰出的几何学家莱布尼兹的通信中，我表明我已经知道确定极大值和极小值的方法、作切线的方法以及类似的方法，但我在交换的信件中隐瞒了这些方法……这位最卓越的科学家在回信中写到，他也发现了一种同样的方法。他并叙述了他的方法，它与我的方法几乎没有什么不同，除了他的措辞和符号以外。”但在第3版及以后再版时，这段话被删掉了。因此，后来人们公认牛顿和莱布尼兹是各自独立地创建了微积分的。

牛顿从物理学出发，运用集合方法研究微积分，其应用上更多地结合了运动学，造诣高于莱布尼兹；莱布尼兹则从几何问题出发，运用分析学方法引进微积分概念，得出运算法则，其数学的严密性与系统性是牛顿所不及的。莱布尼兹认识到好的数学符号能节省思维劳动，运用符号的技巧是数学成功的关键之一。因此，他所创设的微积分符号远远优于牛顿的符号，这对微积分的发展有极大的影响。1713年，莱布尼兹发表了《微积分的历史和起源》一文，总结了自己创立微积分学的思路，说明了自己成就的独立性。