微积分的萌芽与先驱工作-《数学文化选粹》

1．古代东方微积分的萌芽

战国时代的《庄子·天下篇》中，“一尺之锤，日取其半，万世不竭”潜含无限思想。“至大无外，谓之大一；至小无内，谓之小一”，这是惠施（约公元前370—前310）的一句话，提出了无穷大与无穷小的概念。

此外，当时的重要著作《墨经》中不仅对有穷与无穷作了明确的区分，而且也有丰富的微分思想。

我国三国时期（公元3世纪）的数学家刘徽在《九章算术》的注文中，第一次把《庄子》中的极限思想用于算“圆天”和“弧天”的面积，创立了一种推求圆周率的方法，即“割圆术”。刘徽先在圆内作内接正6边形S6，S6的面积不难算出。再继续算出正12边形，正24边形……他指出：“割之弥细，所失弥少。割之又割，以至于不可割，则与圆合体，而无所失矣。”这等同于现代微积分中的极限思想。他得出了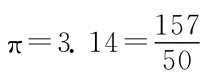（徽率）。

古印度数学家对圆则采用了类似于切西瓜的方法，把圆切成许多小瓣，再把这些小瓣对接成一个长方形，用长方形的面积去代替圆的面积。

2．古希腊、罗马微积分的萌芽

古希腊的原子论者德谟克利特就具有朴素的微分和积分思想。

圆是最美也是最重要的曲边形，古埃及人把它看成是神赐予的神圣的图形。如何求圆的面积是数学对人类智慧的一次考验，也是极限诞生的种子。

大约在公元前400年古希腊人就提出了3大几何难题，其中之一就是“化圆为方”，即指用圆规与无刻度的直尺求与一圆等面积的正方形。

这一几何难题直到19世纪，才被人们证明为尺规作图所不能解决的问题。既然化圆为方这条路走不通，人们不得不开动脑筋另觅他途。公元前5世纪的古希腊智者安提丰与布拉森分别用圆的内接多边形以及外切正多边形的边数不断加倍的办法来接近圆的面积。他们认为圆的面积可以取为：当边数不断增加时，圆的内接和外切正多边形的面积的平均值。这可能是西方应用极限面积计算圆面积的最早设想。对这一思想做出重大发展的是欧多克斯，相应的方法被后人称为“穷竭法”。这一方法被欧几里得记述在《几何原本》第12章中，继欧多克斯、欧几里得之后，阿基米德对穷竭法做出了重要贡献，这位“数学之神”证明了3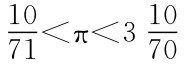，还计算出了球的体积和表面积、抛物线弓形的面积等。

虽说穷竭法发展到阿基米德可谓达到了高峰，但由于当时没有变量的概念，没有引入数值的计算，该方法完全束缚在几何形式之中；当时也无完整的符号系统，只能完全用语言来叙述，所以穷竭法使用极不方便，自阿基米德之后，在相当长的时期内便无人注意。

3．西方微积分的先驱工作(www.xing528.com)

到了17世纪，德国天文学家开普勒在1615年出版了《葡萄酒桶的立体几何》一书，书中介绍了一种他独创的求面积的新方法：把圆分割成许多小扇形。不同的是他一开始就把圆分成无穷多个小扇形，因为太小了，所以小扇形又可用小等腰三角形来代替。

他还利用阿基米德的“穷竭法”求出387种旋转体的体积。

继开普勒之后，意大利物理学家伽利略的学生卡瓦列里深入地研究了上述求积的方法。他想：开普勒为什么不再继续分下去呢？要是真的再细分下去，那分到什么程度为止呢？陷入深思之中的卡瓦列里从衣服的布和一本书的构造上得到了启示，经过反复琢磨，提出了求面积和体积的新方法——不可分元法，并于1635年在意大利出版了《不可分量几何学》一书。

这可以说是积分学的先驱工作，其中“不可分元法”被认为是当时最好的“求积”方法之一。联想定积分、二重积分的定义以及微元法，我们都会发现它们有着千丝万缕的联系。

十六七世纪的自然科学提出了大量的数学问题，微分学主要与以下两个问题相联系：求曲线在任意一点的切线和求变量的极值。

1650年左右，法国数学界3巨头——罗伯瓦尔（Gilles Persone de Roberval， 1602—1675）、费马（Pierre de Fermat，1601—1665）和帕斯卡（Blaise Pascal，1623—1662），对这两个问题作了深入的研究。罗伯瓦尔借助合成运动速度作切线，他从运动的角度出发，将切线看作是描绘曲线的运动在这点的方向，解析几何的焦点重合时的割线。费马则从集合的角度出发，认为切线是当两个交点重合时的割线。费马还借助微小增量作切线，此外他对求变量的极值问题也提出了较好的方法（即先求f′（x），再令f′（x）＝0解之即为极值点）。

这里主要介绍帕斯卡、瓦里士（John Wallis，1616—1703）和巴罗（Barrow，1630—1677）的工作。

帕斯卡在积分学上用“无穷小矩形”取代了卡瓦列利的“不可分元”，算出了以曲线y＝x2为曲边的曲边形面积；在微分学上，他把无穷小概念引入数学，出版了《四分之一圆的正弦论》（1659）。事实上，他的工作对莱布尼茨的微积分产生了直接的影响。25岁时，当他正享有科学家的盛誉时，竟突然决定放弃这些科学研究，献身于哲学和宗教，这种难以理解的行动，不能不说是科学界的极大损失。

瓦里士是英国最富独创性的数学家之一。他早年在剑桥大学学习神学，从1649年起是牛津大学的“沙维教授”。在微积分的先驱者中，瓦里士的算术化工作很有意义：可以说，没有算术化就没有牛顿的微积分。他的著作《圆锥曲线论》与《无穷小算术》都是很有名的。他第一次用符号∞表示无穷大，用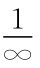表示无穷小或零量，并把它们与有限数同样地看待，一起参加运算。他还引入了“变量极限——这是变量所能如此逼近的一个常数，使得它们之间的差能够小于任何给定的量”，经过复杂的推理，算出：

对牛顿影响最大的是他的老师——英国的伊萨克·巴罗，他也是微积分发展史上重要的人物之一，精通希腊文和阿拉伯文，曾任剑桥大学教授、副校长。1669年，即牛顿26岁那年，巴罗主动宣布牛顿的学识已经超过了自己，并把“路卡斯教授”的职位让给牛顿，其主要著作为《光学和几何讲义》（1669）。他偏爱几何，对即将临产的微积分也有深刻的理解，曾设想曲线是由所谓的“线元”构成的。他最有意义的贡献就是把“求切线”和“求积”作为互逆问题联系起来。

经过薄暮、黑夜和黎明，这一神秘的时代以费马和巴罗为标志结束，这时微积分的诞生已经到了水到渠成的阶段，就像窗户纸一样一捅就破。自然上帝将这一重任委以牛顿与莱布尼茨。