古希腊数学学派：数学文化探秘

古希腊是由众多以公民集体为主导的城邦国家组成。古典时期的希腊数学，相继集中于几个中心地点的城市，并形成了几大数学学派。

1．爱奥尼亚学派

第一个学派是米利都地区以古希腊数学先行者泰勒斯为首的爱奥尼亚学派。

泰勒斯本人早年经商，往返于埃及和巴比伦等地，学到不少天文学和几何知识，养成了精明严谨的学者风度，崇尚自由，不愿受宗教信条的约束。他预报过公元前585年的一次日食，利用日影测量过金字塔的高度。他最早提出定理必须证明的思想，开创了几何证明的先河，并促成希腊数学从直观的感性经验阶段向抽象的理性证明阶段过渡，进而向几何公理化方向发展，由此奠定了希腊数学的基础，成为数学发展史上第一个重要的里程碑。他被后人尊之为“世界上第一位数学家”，并把他与柏拉图、苏格拉底、亚里士多德、毕达哥拉斯、欧几里得和阿基米德合称为“希腊七贤”，他则为七贤之首。

2．毕达哥拉斯学派与第一次数学危机

继爱奥尼亚学派之后，是形成于意大利南部的毕达哥拉斯学派。学派首领毕达哥拉斯曾就学于泰勒斯名下，并游历过埃及和巴比伦。他早年在家乡萨摩斯从诗人克莱菲洛斯那里学习过诗歌和音乐。在古希腊人那种与生俱来、永不满足的好奇心的驱使下，他对音乐情有独钟，并从中看到了数学，他甚至深信能用数学公式去解释世间的各种事物和现象。后来，他在克罗顿成立了一个集科学、宗教和哲学于一体的帮会性质的半公开的学术团体。虽然该学团在与贵族党结盟反对民主派的政治斗争中失败，毕达哥拉斯本人也于公元前497年被杀，但他的信徒们分散到希腊各地的学术中心，继续贯彻落实学派的宗旨，直到公元前400年左右，前后延续了近两个世纪。

毕达哥拉斯学派的数学观念带有浓厚的原始文化的数学神秘色彩。亚里士多德曾说，毕达哥拉斯学派把数看做是真实物质对象的组成部分。这种“万物皆数”的观点构成了毕达哥拉斯学派的核心观念。

据传，毕达哥拉斯学派关于谐音的研究对于其核心观念的形成起到了十分重要的作用。他们发现，弹弦音质的变化来源于弦长短的数量变化，两根绷得同样紧的弦如果长度成正比，那么就会发出谐音。既然音乐这种似乎与数毫无联系的现象最终都可以用数来解释，这也就极大地增强了毕达哥拉斯学派用数来解释世界的信心。

由上述信念出发，毕达哥拉斯学派进而又提出了行星的运动也可用数的关系来表达。由于认为物体在空间运动时会发出声音，运动快的物体比运动慢的物体发出的声音高，因此毕达哥拉斯学派认为，行星的运动最终也可以通过“天际”的音乐表示为数量关系。离地球越远的天体运动越快，各个行星则因其离开地球距离的不同而发出的声音匹配为和谐之音，等等。

第一次数学危机

毕达哥拉斯的数是指整数，他们在数学上的一项重大发现是证明了勾股定理。他们知道满足直角三角形三边长的一般公式，但由此也发现了一些直角三角形的三边比不能用整数来表达，也就是勾长或股长与弦长是不可通约的。这样一来，就否定了毕达哥拉斯学派的信条：宇宙间的一切现象都能归结为整数或整数之比。不可通约性的发现引起了第一次数学危机。

这个发现对古希腊的数学观点有极大的冲击。这也表明，几何学的某些真理与算术无关，几何量不能完全由整数及其比来表示。反之，数却可以由几何量表示出来。整数的尊崇地位受到挑战，于是几何学开始在希腊数学中占有特殊地位。

同时这也反映出，直觉和经验不一定靠得住，而推理证明才是可靠的。从此，希腊人开始由“自明的”公理出发，经过演绎推理，由此建立几何学体系，这不能不说是数学思想上的一次巨大革命，这也是第一次数学危机的自然产物。

综观毕达哥拉斯学派的研究，我们可以清楚地看到人们对数学神秘性的继承和发展。但是，这种神秘的数学研究却把人们对世界的认识和理解引向了一条数学化的道路。首先，纯粹的数学研究应首先归功于毕达哥拉斯学派；其次，毕达哥拉斯学派对数的研究则是人类第一次用数来研究世界、研究自然的本质，是人类第一次企图从数与数的关系上来解释世界、解释自然。

3．埃利亚学派与芝诺悖论

对于更后一些出现的埃利亚学派，保留下来的史实不多。该学派位于意大利南部的埃利亚城，其代表人物是芝诺（Zeno）。由于毕达哥拉斯学派的不可公度线段的发现，说明长度并不是度量单位的离散集合，而是一个连续的量，面积、体积和时间等无不如此，这就突出了离散与连续之间的矛盾。

大约公元前450年左右，大诡辩家芝诺是当时巴门尼德（哲学家）的学生，他为此提出了4个关于运动的悖论，它们都是针对空间和时间是无限可分还是由不可分的小段组成而提出来的，不论在数学史上还是在哲学史上、逻辑史上皆有过重要贡献，也是第二次数学危机的导火线之一，主要揭示了离散与连续之间的关系，并曾对后世产生过深远的影响。这里举出其中的3个悖论。

（1）二分法疑难

“运动是不存在的”。比如说物体从A移动到B，按常理，从A到B之前需要先到AB的中点C，需要到达C之前又必须到达AC的中点D，……如此下去，显然有无穷多个这样的中点。第一，每找一个中点都需要时间，故对无穷多个中点需时间也是无穷的，即永远找不到距A最近的一个中点，亦即这个点不存在。第二，物体欲从A到B，又非经过这个最近的中点不可。结论是物体运动是不可能的。而常识告诉我们物体是运动的，这样就相互产生了矛盾！

无独有偶，在我国战国时期，也有个因为精于辩论的人物叫惠施。他很有学问，传说他写的书要装好几大车，他有一句名言“一尺之棰，日取其半，万世不竭”，意思完全与上类同。

这个悖论用极限解释是很简单的，即设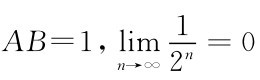，所以距A最近的中点就是其自身，因此超越自己就运动了。

（2）阿其里斯悖论

这是芝诺最著名的一个诡辩，采用通俗的方式叙述就是：假设乌龟和阿其里斯赛跑（阿其里斯是希腊神话中的神行太保），只要乌龟的起跑点领先一段距离，芝诺说阿其里斯永远也追不上乌龟。比方说，人的速度是乌龟的10倍，即v阿＝10v龟，又假设乌龟在人前面100米处起跑，当阿其里斯跑了100米，到达乌龟的出发点时，乌龟已向前爬了10米；阿其里斯再追10米，乌龟又爬了1米；阿其里斯又追了1米，乌龟又爬了0．1米……这样如此下去，以至无穷。他们永远相隔一小段距离，换言之，阿其里斯总在乌龟之后，即他永远也追不上乌龟。

这反映了连续与离散的矛盾！事实上，设v阿＝10米／秒，v龟＝1米／秒，AB＝100米，这时，由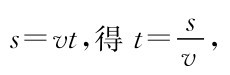

所以

由无穷级数理论得到，上述和是一个公比为0．1的等比级数，｜0．1｜＜1，因此收敛。

（3）飞矢疑难

“飞矢不动”，理由是飞矢在任何一个时刻只能占据空间的一个特定的位置，即在这一瞬间，他就静止在这个位置上。所以，飞矢的所谓运动，只是许多静止的总和，因此，飞矢不可能动。其实，物体在某一时刻运动与否，现在我们知道决定于它的瞬时速度，而与其所在的位置无本质关系。

芝诺的3个诡辩论都反映了连续与离散、无穷小与很小很小的矛盾。它们与后来贝克莱、格兰弟等的悖论以及非欧几何的真理性问题导致了第二次数学危机。

该学派还有关于数、几何、连续直线和立体体积方面的有关著作，书中甚至记载了圆锥与棱锥的体积是同底等高的圆柱与棱柱体积的1／3。这些著作成为欧几里得《几何原本》问世之前希腊数学的重要著作。(www.xing528.com)

4．诡辩派

另一个学派——诡辩派，又称为智人学派，是在希腊城邦联盟的中心城市雅典成立的第一个学派，其中不乏各方面的学者和大师。数学方面的代表人物有希比阿斯和安提丰。该学派提出并研究了三等分任意角、化圆为方和立方倍积三大几何作图问题，并且只允许用圆规和无刻度的直尺作出它们。其实，这些问题的解决已大大超越了当时数学发展的实际水平。最终，这几个问题经过历代数学家的苦苦探寻，直到19世纪才陆续以否定的形式获得答案，但其严格证明不是用几何方法而是用代数方法完成的。

如果取消作图工具的限制，三大作图问题都能迎刃而解。实际上早在公元前425年，该学派的希比阿斯就发明了一种“割圆曲线”用以解决化圆为方的问题。公元前400年左右，希波克拉底和欧托修斯共同把立方倍积问题转化为线段之比，用木工方尺解决了它。公元前240年左右，阿基米德又用阿基米德螺线解决了三等分任意角的问题。

智人学派的不少数学成果都是为解决三大作图问题而得来的副产品。其中，安提丰在研究化圆为方问题时，最早想到用边数不断增加的多边形的面积去近似趋近于圆的面积的极限思想，为后来“穷竭法”的提出奠定了基础。

5．柏拉图学派

继智人学派之后，在希腊数学中居主导地位的是雅典的柏拉图学派。由于该学派领袖柏拉图的两位老师是毕达哥拉斯学派的学者，所以该学派受毕达哥拉斯学派的影响很深。

柏拉图出身贵族，是当时希腊著名的哲学家，被誉为那个时代“最有学问的人”。他曾拜师于苏格拉底，在其门下学习了8年，当苏格拉底被雅典的民主政权处死之后，他开始了长达12年的流亡生涯。

公元前387年，他用万贯家产创办了雅典学院，学院大门的横额上写着“不懂几何者，不得入内”。数学和哲学是学院中最受欢迎的两门学科。柏拉图虽不是数学家，但却十分热爱数学，关心数学研究。公元前4世纪前后，希腊数学中的所有重要工作，几乎都是他的朋友和学生做出的。他的学院一直存在了约900年。

作为一个哲学家，柏拉图突出地强调了数学对于哲学与了解宇宙的重要作用。柏拉图认为，存在着一个物质的世界——地球以及其上的万物，通过感官我们能够感觉到这个世界；同时，还存在着一个精神的世界，一个诸如美、正义、智慧、善、完美无缺和非尘世的理念世界。感官所能把握的，只是具体的和逝去了的东西，只有通过心灵才能达到对这些永恒理念的理解。这些就是柏拉图哲学的核心。

与毕达哥拉斯学派一样，对柏拉图来说，世界是按照数学来设计的。柏拉图试图对世界的本原做出进一步的具体论述。他指出，构成物质世界的真正元素并不是土、气、火与水等具体物质，而是5种正多面体，因为这些元素的每一个原子都是正多面体。土的原子是立方体，火的原子是正四面体，气的原子是正八面体，水的原子是正二十面体，另外正十二面体对应的则是宇宙。这样，在柏拉图那里，数学就成为了构造世界的基石。柏拉图对数学重要意义的突出强调，极大地激励了和他同时代的人以及后人从事数学的研究。

柏拉图的学生亚里士多德是该学派继柏拉图之后最优秀的代表，被誉为古希腊“最伟大的思想家”。他最早提出数学定义链中必有无定义的“原始”概念，数学推理中命题链的出发点是公理与公设，使数学推理变得严格而规范。他是“亚里士多德三段论”的创始人，他还给出了矛盾律和排中律，构建了数学中间接证法的逻辑基础，破天荒地创立了形式逻辑学，为曾就学于雅典学院的欧几里得建立自己的几何体系奠定了深厚的思想和逻辑基础。不仅在欧几里得的《几何原本》中有几个定理是属于他的，而且他还明确地提出点和数是离散量，必须同几何中的连续量加以区别。他建议讨论无限这一概念时，把潜在的无限与真实的无限区别开来。从公元前335年开始，他离开柏拉图学派，成立了自己的学园学派，进一步拓展了自己的研究。其著作涉及机械、物理、数学、逻辑、动植物、心理、伦理、文学、经济等众多学科领域。他告诫我们：“全凭思考不可能找出最佳方案。我们需要的是观察与经验，加上逻辑推理和直觉。”

在柏拉图学派中还有一位数学家是必须提到的，那便是欧多克索斯。他是古希腊几位最杰出的数学家之一，同时又是一位天文学家、地理学家和医生。有关天体运动的第一个天文学说就是由他创立的。在数学上，他提出了关于比例的新理论，为无公度线段的处理提供了逻辑依据，为希腊数学的研究重点由算术转向几何创造了条件。他发明了计算曲边形面积和曲面体体积的方法——穷竭法，并用这一方法证明了两圆面积之比等于半径的平方之比，两球的体积之比等于半径的立方之比，表明他已萌生了极限及积分的思想。他甚至已着手进行数学上以自明的公理为依据开展演绎推理的逻辑建构工作。

6．亚历山大学派

公元前338年，希腊地区被马其顿统一，建立了托勒密王朝，定都在亚历山大城。从此，希腊数学的中心也从雅典转移到亚历山大。

这座以马其顿君主名字命名的城市，在公元前3世纪时，修建了宏伟的博物馆和图书馆。从那时起到公元前30年的300年左右的时间，是希腊数学的鼎盛时期。欧几里得、阿基米德和阿波罗尼奥斯联手在亚历山大组建起亚历山大数学学派，并陆续取得一系列极其伟大的数学成就。

欧几里得治学严谨，鄙弃功利和投机取巧的学风。他从年轻时起，就养成重视逻辑推理与证明的习惯，并对几何学表现出极高的造诣。托勒密国王得知这一消息后，邀请他客居亚历山大城，并向他学习几何学。于是他长住亚历山大，潜心著书立说。他继承了泰勒斯、毕达哥拉斯、柏拉图及其学派的“论证数学”和公理化思想，细心搜集整理、研究总结希腊古典时期的数学成果，终于写出了数学史上里程碑式的鸿篇巨著——《原本》。因明末科学家徐光启首次翻译此书时，将该书的中文名称定为《几何原本》，故我国一直沿用这一书名。无疑，托勒密王朝开明的政治和对科学发展的重视是《原本》赖以产生的决定性因素。本章的后面将对其进行详细介绍。

由于在亚历山大时期，有文化的奴隶主阶级与受奴役的奴隶阶级之间的隔离和壁垒被突破，有文化素养的人也开始关心实际事务。数学研究的内容，由几何知识拓展到数量知识，进而发展了算术和代数。阿基米德（Archimedes，前287—前212）的工作足以说明这样的转变。

阿基米德是欧几里得的学生，既是一位伟大的数学家，也是一位伟大的物理学家，是超越他那个时代的一位天才。他自幼在父亲的辅导下钻研《原本》，后来成为亚历山大学派的成员。他兴趣十分广泛，并且有非凡的机械运用技巧。他第一次明确地给出，并用“穷竭法”证明了圆的面积为该圆周长与半径乘积之半；他求出抛物线与一直线相交围成的平面图形的面积是同底（以直线段为底）等高的三角形面积的4／3；他计算出球面面积是其大圆面积的4倍或该球的外切圆柱体表面积的2／3，球的体积是外切圆柱体体积的2／3；牟合方盖的体积是其外切立方体体积的2／3等一系列重要结果。

他的著作文字优美，构思巧妙，论证严密，技巧性强。他常常将力学原理用于数学解题之中，创造出一种解数学题的数学—力学方法，构思之奇特令人称绝。例如，他在计算球体体积时，就用了这一方法。从本质上讲，他的方法中已经包含了在两千年以后才出现的极限与积分的思想。在谈到他论证的严密性时，克莱因说：“他的严密性比牛顿与莱布尼兹著作中的高明得多。”莱布尼兹则说：“了解阿基米德与阿波罗尼奥斯的人，对后代杰出人物的成就就不会那么钦佩了。”就连大文学家伏尔泰都称赞道：“阿基米德头脑里的想象力比荷马头脑里的要多。”

阿基米德流传下来的著作很多，其中最著名的有《圆的度量》《抛物线图形求积法》《论螺线》《论球与圆柱》《论劈锥曲面与旋转椭球》《方法》《论平面图形的平衡或其重心》《浮体论》《砂粒计算》《牛群问题》等。研究希腊数学的权威希斯在20世纪出版的《希腊数学》一书中评论道：“这些著作无一例外地都能视为数学论文的纪念碑。解题步骤的循循善诱，命题次序的巧妙安排，严格摈弃叙述的枝蔓及对整体的修饰润色。总之，给人的完美印象是如此之深，使读者油然而生敬畏之情。”

尤其令人称奇的是，阿基米德一反古希腊轻视应用的传统，找到了数学的用武之地。他的许多著作都是直接针对应用的。他根据螺线理论发明制作的农用水车，现在仍在埃及农村中使用。他坚定地认为：“力学便于我们发现结论，而几何则能帮助我们对结论做出证明。”

阿基米德在让数学研究与实际联系的过程中，既注重数学联系实际，让数学为现实服务，解决实际问题；又注重实际靠近数学，让现实为数学服务，发展数学。这位伟大的科学先知，在第二次布匿战争中惨遭罗马士兵杀害。

阿波罗尼奥斯出生于小亚细亚，同样是欧几里得的学生。他在欧几里得之后，整理和发掘希腊古代数学知识方面做了大量工作。他专攻几何，写下了6卷集的《圆锥曲线论》。该书具有与《原本》一样严谨的风格和十分明显的解析法的思想。书中在《原本》10个公理的基础上共列出487个命题，经过一千多年的时间，竟无人对其进行增补或修改。直至笛卡儿的《解析几何》一书问世，在有关圆锥曲线的理论方面始终无人能超越。

古希腊的最后一位数学家（同时也是一位数学评注家）是帕普斯。他认真收集并注释了在他以前的古希腊数学家的经典著作，写成八大卷的《数学汇编》。当然，书中还包含了他本人的创造性工作。比如，关于平面等周问题的定理：“周长相等的平面图形，以圆的面积为最大。”射影几何中的帕普斯定理：“若A、B、C是一直线上的3点， A′、B′、C′是另一直线上的3点，则AB′与A′B，BC′与B′C，以及AC′与A′C相交的3点X、Y、Z共线。”以及关于旋转体体积的帕普斯定理：“平面图形绕同一平面上的轴线转动形成的立体的体积等于该图形的面积与以其质心所画圆的周长之积。”该书不仅集希腊几何发明创造之大成，而且也是我们现在所能见到的古希腊数学名著中的最后一部著作。所以，中国科学技术大学数学系的王树禾教授称它为“古希腊诸位著名数学家的安魂曲。”

随着罗马帝国的兴盛，灾难开始降临到希腊人头上。公元前146年罗马人征服了希腊本土；公元前64年罗马人又占领了美索不达米亚；公元前47年独裁者恺撒纵火焚毁停泊在亚历山大港的埃及舰队，大火延续到城内，烧掉了亚历山大图书馆，长达250多年的藏书和50万份手稿被毁于一旦。贪婪的罗马君王把他所控制的每个国家都搞得民穷财尽，富庶的希腊各城邦当然首当其冲。

由于罗马人的入侵，大约从公元l世纪初起，亚历山大的数学研究工作，特别是在几何研究方面开始衰落，那时数学家们只是忙于阐释和挽救先前数学家们的著作，很少再有新的发现，由于战火不断，即使是这样的日子也并未持续多久。

罗马人把基督教奉为国教，这就为摧毁希腊文化提供了条件。神庙被改为教堂，希腊本土的异教徒受到驱逐和屠杀，全世界第一位著名的女数学家许波提娅的悲惨遭遇便是一例。在基督教里教徒们是绝对不准沾染上希腊学术这个“脏东西”的，他们把数学与“恶行”同等看待，制订出《数学与恶行禁典》，以法律形式禁止数学知识的传承。由于独裁者政治上的需要、教徒们的愚昧无知，给辉煌的希腊数学带来了灭顶之灾。神庙中仅存的一些希腊数学图书及手稿全部被烧。529年，所有希腊哲学学校全被东罗马王杰斯丁宁封闭，学者们被迫离散。后来，新崛起的阿拉伯征服者在640年征服埃及，又给地处埃及的亚历山大城以最后的打击。亚历山大的浴堂里，有足足半年时间用写满数学手稿的羊皮纸烧水，最后残留下来的书籍再次被阿拉伯征服者彻底毁灭。野蛮和不学无术又一次彻底摧毁了古希腊文化。

当然，古希腊数学的局限性也成为制约它进一步发展的重要因素。大家一致公认，希腊人把数学抽象化、演绎化、公理化、艺术化，在算术与代数的推广、平面与立体几何、平面与球面三角的建立及数论方面的开创性工作中成就显赫，功不可没；但他们把数学作为心智的艺术，灵魂的音乐，使数学长时间脱离生活实际这一赖以生存和发展的真正基础。古希腊数学在发展中没有关于无理数的严格理论，研究重点由算数和代数转向几何，并严格限制其研究范围，增大了证明问题的难度。由于过分强调严谨，失去了不少创造和发明的途径与机会；由于对无穷的望而生畏，使之与变量和极限失之交臂；加上唯心主义先验论的哲学思想指导，这一切使希腊数学在经历了一千多年的辉煌之后，因受到内外双重因素的影响，终于在历史上销声匿迹，古希腊的文明在其行将跨入近代文明之际不幸夭折了。