中国古代数学发展的三个关键节点

魏晋时期是继两汉之后我国数学发展的又一高潮时期，出现的玄学不为汉儒经学束缚，思想比较活跃；它诘辩求胜，又能运用逻辑思维，分析义理，这些都有利于数学从理论上加以提高。吴国数学家赵爽的《周髀算经注》中最精彩的就是“勾股圆方图注”。他提出用弦图证明勾股定理和解勾股形的5个公式；在“日高图及注”中，他用图形面积证明汉代普遍应用的重差公式。赵爽的工作是带有开创性的，在中国古代数学发展史中占有重要的地位。魏末晋初刘徽撰写的《九章算术注》《九章重差图》都是出现在这个时期。赵爽与刘徽的工作为中国古代数学体系奠定了理论基础。

我国发现勾股定理比希腊人早500年左右，但证明又要晚800年左右。第一位证明勾股定理的便是西晋时期（公元3世纪初）的赵爽，他是中国古代对数学定理和公式进行证明与推导的最早的数学家之一。他仅用500余字，就列出了关于勾股定理的命题及其证明21条，如图2－1所示就是其中一种证明该定理的方法，用现代符号书写出来即为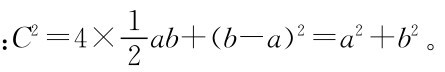

图2－1 勾股定理证明示意图

阮元在《畴人传》一书中评价说：“（这一证法）精深简括，诚算氏之最也。”

刘徽大约与赵爽同时代，出生于公元263年前后，主要的数学著作是《九章算术注》和《海岛算经》（原为《重差》）。他继承和发展了先秦时期儒家和墨家的思想，主张对一些数学名词特别是重要的数学概念给以严格的定义，认为对数学知识必须进行“析理”，才能使数学著作简明严密，利于读者。他的《九章算术注》不仅纠正了原书中的错误，对《九章算术》的方法、公式和定理进行了一般的解释和推导，而且还在论述的过程中有了很大的发展，把《九章算术》的理论水平大大提高了一步，使之成为我国古代数学的奠基性著作之一。刘徽对无理数已有深入的认识，他认为“凡开积为方，方之自乘当还复其积分。令不加借算而命分，则常微少；其加借算而命分，则又微多，其数不可得而定，故以面命之，为不失耳。”这其实已是一种近似逼近的思想，不足之处仅在于未能严格证明“面”的存在。刘徽与欧几里得一样擅长几何，并“以六觚（古代酒具，觚口为正六边形）之面割之又割，以求周径相之为率”求出π＝3．1416，这已是十分精确的结果了，后人称它为徽率。他提出的“割之弥细，所失弥少，割之又割，以至于不可割，则与圆周合体而无所失矣”的思想，与17世纪欧洲人的极限思想异曲同工，如出一辙。刘徽用无穷的、分割的方法证明了直角方锥与直角四面体的体积比恒为2∶1，解决了一般立方体体积的关键问题。在证明方锥、圆柱、圆锥、圆台的体积时，刘徽为解决球的体积问题提出了正确途径。

刘徽的《海岛算经》是有关“重差术”（相当于欧洲近世的“三角术”）的专论，原附于《九章算术注》之后，是唐初（公元7世纪）才从中抽出来另成一书的。

刘徽非常看重图形直观在数学研究中的重要作用，主张研究数学要“析理以辞，解体用图”，既重视抽象思维的“析理”，又重视直观形象的“用图”，这在当时是十分难能可贵的。

刘徽厌恶政治统治的残暴和教育制度的腐朽，感慨“当今（对数学）好之者寡，故世虽多通才达学，而未必能综于此耳。”上述成就的取得与他不贪图荣华富贵，一辈子潜心研究数学是分不开的。我国政府于2002年特别发行了刘徽的纪念邮票，此举表明他是我国公认的文化名人之一。

东晋以后，中国长期处于战争和南北分裂状态。祖冲之父子的工作就是在经济、文化南移以后，南方数学发展的具有代表性的工作。祖冲之（429—500）是南北朝时期南朝一位杰出的数学家，同时也是天文学家和机械师。他博学多才，著作颇丰。在数学方面有《缀术》6卷，《九章述义注》9卷和《重差注》1卷，另有“小说”10卷，只可惜这些书都已失传。原因是“（唐朝）学官莫能查其深奥，是故废而不理。”从《南齐书》《南史》和《隋书》中的记载可知，他用穷竭法计算出3．1415926＜π＜3．1415927，后人称它为祖率（直到1429年才由伊朗人打破这一记录），另有密率和约率分别为355113和227。祖冲之的这一工作，使中国在圆周率计算方面比西方领先约1000年之久。

关于圆周率的计算，我们不要小看上述结果，一位德国数学家讲得好：“历史上一个国家所算得的圆周率的准确程度，可以作为衡量这个国家当时数学发展水平的一个标志。”

从公元前3世纪以来，数学家们一直前仆后继，苦苦探寻，计算π的更为精确的值。

在电子计算机问世之前，用人工算到了707位小数；电子计算机问世之后，短短40年，就把计算精度提升到了2×1011多位小数，它的强大功能已使这一计算失去了原有的意义。根据π值的超越性，再如此算下去似乎没有太多必要了。

在天文学方面，祖冲之编制了当时最为科学和实用的《大明历》，算出了一个回归年为365．2428日（实为365日5时48分46秒），并对木星公转周期和岁差理论研究有着重要贡献；在机械制造方面，他设计制造过水碓磨、千里船和指南车等。

图2－2 π值图

我国邮电部1955年发行了祖冲之的成套邮票，1959年苏联宇宙火箭在月球上发现的环形山被命名为“祖冲之山”，我国紫金山天文台还把1964年11月9日发现的小行星也命名为“祖冲之星”，足见其在世界文化史上所处的重要地位。

祖冲之之子祖暅总结了刘微的有关工作，提出了“幂势既同则积不容异”，即等高的两立体，若其任意高处的水平截面积相等，则这两立体体积相等，这就是著名的祖暅原理。祖暅应用这个公理，解决了刘微尚未解决的球体积公式。这一公理在西方被称为卡瓦列利原理。但卡瓦列利是17世纪的人，我国早在公元3世纪已由刘徽加以应用，而在公元6世纪由祖暅十分清楚地提出来了。我们称他为刘祖等积定理或祖暅原理。祖暅还继续刘徽的工作，算出牟合方盖（两个底圆半径相等的直交圆柱面围成的封闭立体）的体积(www.xing528.com)

图2－3 牟合方盖

隋炀帝好大喜功，大兴土木，客观上促进了数学的发展。其中最值得提及的数学家便是张遂，数学著作是《十部算经注释》，数学教育是“国子监”的创立。

张遂是唐代的一位高僧，法名一行。他自幼聪明好学，博览群书，青年时便以学识渊博著称。他性情耿直，藐视权贵，从不趋炎附势，为躲避武则天侄子的纠缠，他毅然削发为僧，隐居嵩山，直到721年，受唐玄宗之命才出山主持新历编制。他苦干两年写成了《大衍历》，该历法从729年开始在全国实行，后传入日本，日本使用此历法达百年之久。在历法编制的过程中，为进行相关计算，他还创造出正切函数表，并在隋代天文学家刘焯的等间距二次内插法的基础上总结出不等间距二次内插公式，为我国计算方法的发展树起又一根标杆。这比牛顿发明的二次内插法足足早了1000年。

经隋唐300多年的发展，中国的数学得到了空前繁荣。历代留存下来的有代表性的数学著作多达三四十种，其中最有名的能较好地反映中国古代数学完整体系及发展水平的著作，当推李淳风等人奉命注释的“十部算经”。这十部算经包括《周髀算经》《九章算术》《海岛算经》《孙子算经》《张丘建算经》《五曹算经》《五经算术》《缉古算经》《数术记遗》《夏侯阳算经》。它们被当时选定为国子监学习和参加科举考试的必读之书，也成为现在研究从汉代到唐代千余年间中国数学发展全貌的宝贵资料。

《孙子算经》分上、中、下三卷，上卷为筹算乘除法，中卷为筹算的分数运算及开平方法，下卷则为一些算术难题的解法。“鸡兔同笼”“韩信点兵”都是其中的典型问题。

《五曹算经》《五经算术》和《数术记遗》成书于南北朝时期，其中《五曹算经》是为五类官员编写的，共分为五卷。田曹讲田亩面积的计算，兵曹讲关于军队配置及给养运输的数学问题，金曹讲纺织物买卖及钱财货币的处理问题。

《五经算术》是汉代经学家们对《尚书》《诗经》《周易》《周礼》《礼记》这5部经书中涉及的一些数学知识文句的解释。

《数术记遗》是因为《缀术》失传而用之凑数的一部书，全书带有较为浓厚的神秘色彩，“九官算”就出自该书。

《夏侯阳算经》的现传本中包括我国4～8世纪的许多数学资料（宋代定稿），共分三卷，收入了83个问题。这些问题大多是当时社会实际生活中的各种计算问题。书中已显现出对筹算制度进行改良的倾向。

《张丘建算经》大约成书于南北朝时期，全书共分三卷，其中难度较大的内容是涉及等差级数的计算及一般二次方程的求解，“百鸡问题”便出自该书。

唐初王孝通的《缉古算经》（公元7世纪），全书共讨论了20个数学问题的解法（涉及三次方程多达28处），其中以解决上宽下窄、前高后低的形状不规则的堤坝计算问题最为精彩。其主要讨论土木工程中计算土方、工程分工、验收以及仓库和地窖的计算问题，反映了这个时期数学的情况。王孝通在不用数学符号的情况下，列出数字三次方程，不仅解决了当时社会的需要，也为后来天元术的建立打下基础。此外，对传统的勾股形解法，王孝通也是用数字三次方程解决的。

南北朝开始到隋唐时期，伴随着佛教的流传，中印间文化交流频繁，圆弧的量法、正弦函数表、印度数码等也在这时通过历法编制由印度传入中国。中国数学的成就则经印度传入东亚、西亚和欧洲。

唐初封建统治者继承隋制，656年在国子监设立算学馆，设有算学博士和助教，学生30人。由太史令李淳风等编纂注释《算经十书》，作为算学馆学生使用的课本。明算科考试亦以这些算书为准。李淳风等编纂的《算经十书》，对保存数学经典著作，为数学研究提供文献资料方面是很有意义的。他们给《周髀算经》《九章算术》以及《海岛算经》所作的注解，有利于学生的学习。隋唐时期，由于历法的需要，天算学家创立了类似于今天二次函数的内插法，丰富了中国古代数学的内容。

算筹是中国古代的主要计算工具，它具有简单、形象、具体等优点，但也存在着布筹占用面积大，运筹速度加快时容易摆弄不正而造成错误等缺点，因此很早就开始进行改革。其中太乙算、两仪算、三才算和珠算都是用珠的槽算盘，在技术上有重要的改革。尤其是珠算，它继承了筹算五升十进与位值制的优点，又克服了筹算纵横记数与置筹不便的缺点，优越性十分明显。但由于当时乘除算法仍然不能在一个横列中进行，算珠还没有穿档，携带不方便，因此仍没有普遍应用。

唐中期以后，商业繁荣，数学计算增多，迫切要求改革计算方法，从《新唐书》等文献保留下来的算书书目，可以看出这次算法改革主要是简化乘、除算法，唐代的算法改革使乘除法可以在一个横列中进行运算，它既适用于筹算，也适用于珠算。