动态贝叶斯网络在网络舆情中的应用

本章3.3.1节及3.3.2节介绍的知识主要针对的是静态贝叶斯网络，实际上还有一种结构称为动态贝叶斯网络（Dynamic Bayesian Network，DBN），这里的动态体现在样本数据和观测数据的变化。一般情况下，动态贝叶斯网络具有如下特点：

（1）网络的基本拓扑结构在每个时间片内相同；

（2）片与片之间通过类似的弧相连。

动态贝叶斯网络的概率推导基于静态贝叶斯网络完成，与静态贝叶斯网络推理的不同是在式（3-9）的基础上加上时间信息，此外还需要做出如下假设：

（1）假设在一个时间片内条件概率的变化过程是平稳的；

（2）假设动态概率过程符合马尔可夫过程，即未来时刻的概率仅和当前时刻有关，而与过去时刻没有关系，如式（3-10）所示：

其中，X［1］，X［2］，…，X［n］表示与时间相关的随机变量。(www.xing528.com)

（3）假设相邻时间的条件概率过程是平稳的，即P（X［t+1］|X［t］）与时间t无关。

基于上述假设，可得到动态贝叶斯网络的拓扑结构，该网络包括两部分（如图3-3所示）：①初始网络B0，该网络涉及定义在初始状态X［1］上的概率分布；②转移网络B→，该网络涉及变量X［t］到变量X［t+1］上的转移概率P（X［t+1］|X（t））。

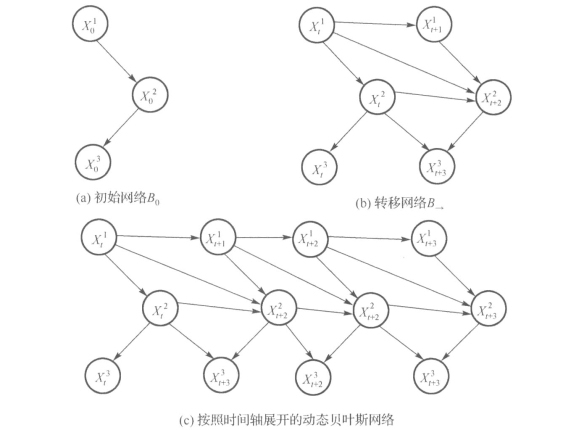
图3-3　动态贝叶斯网络

动态贝叶斯网络在X［1］，X［2］，…，X［n］上的联合概率分布为：

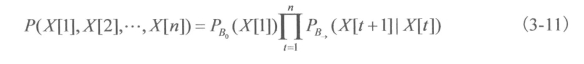
依据上述内容，与基本贝叶斯网络G（V，E）不同，动态贝叶斯网络可表示为由初始网络B0和转移网络B→构成的网络，即表示为（B0，B→）。在B0（3-3（a））和B→（图3-3（b））的基础上，按照时间轴展开可得到图3-3（c）所示的动态贝叶斯网络拓扑结构图。