【摘要】:勾股定理是一个基本的几何定理,指直角三角形的斜边的平方等于两条直角边的平方和。两边的总数是25。用勾股定理,可以快速计算出路径长度,如图3-18所示。图3-18实验10 三角形勾股定理演示使用普通的纸就可以很容易地证明勾股定理,通过动手演示,可以加深你对定理的理解和记忆。图3-19勾股定理A2+B2=C2图3-20三角形边的平方已知A=4,B=3,根据公式A2+B2=C2。可得C2=25厘米,所以C=5,用直尺测量C的长度,看定理是否正确
勾股定理是一个基本的几何定理,指直角三角形的斜边的平方(直角相对的边)等于两条直角边的平方和。
这个公式是这样的:A2+B2=C2,见图3-14。

图3-14
图3-15和图3-16显示了“A”“B”和“C”的“平方”的物理版本。
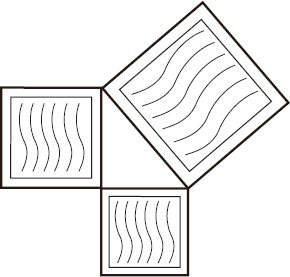
图3-15
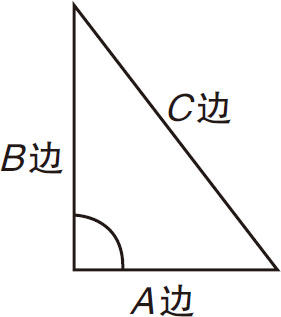
图3-16
在图3-17中显示的三角形,A边是3厘米,B边是4厘米。

图3-17
A边的平方是9,B边的平方是16。两边的总数是25。25的平方根是5。所以,侧边C的边长是5厘米。
用勾股定理,可以快速计算出路径长度,如图3-18所示。

图3-18
实验10 三角形勾股定理演示
使用普通的纸就可以很容易地证明勾股定理(A2+B2=C2),通过动手演示,可以加深你对定理的理解和记忆。(https://www.xing528.com)
需要准备的东西:
►纸
►剪刀
►钢笔
►直尺

制作
在纸上画一个直角三角形,如图3-19所示。对两个直角边进行测量,并计算它们的平方和,如图3-20所示。

图3-19
勾股定理
(适用于直角三角形)A2+B2=C2

图3-20
三角形边的平方
已知A=4,B=3,根据公式A2+B2=C2。
可得C2=25厘米,所以C=5,用直尺测量C的长度,看定理是否正确
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




