数学本来很简单：引导初学者理解几何学

■几何可分为：

欧氏几何学，涉及线、圆、三角形等图形；立体几何涉及立方体、棱柱和金字塔等三维物体。

几何学是关于线条、形状、角度、空间以及它们的属性的学科。

■常见多边形的名称和边的数目：

三角形，3条边

四边形，4条边

五边形，5条边

六边形，6条边

七边形，7条边

八边形，8条边

九边形，9条边

十边形，10条边

十一边形，11边形

十二边形，12边形

十三边形，13条边

十四边形，14条边

■多边形面积的计算公式：

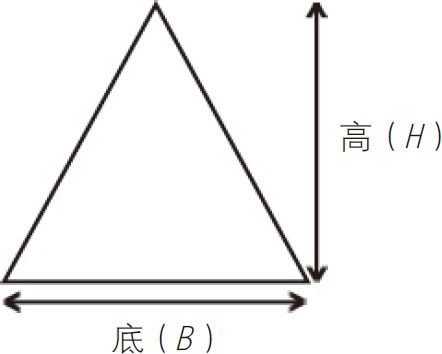
三角形：面积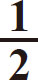＝BH （BH＝底×高）

正方形：面积＝边长的平方

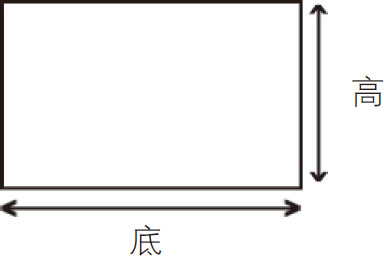
矩形（长方形）：面积＝底×高

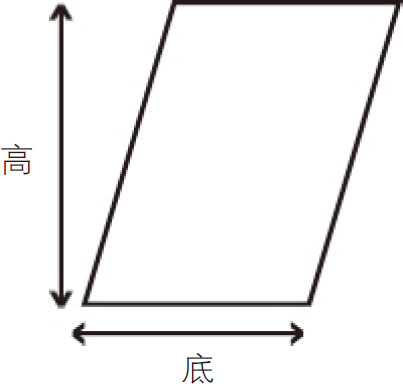
平行四边形或菱形：面积＝底×高

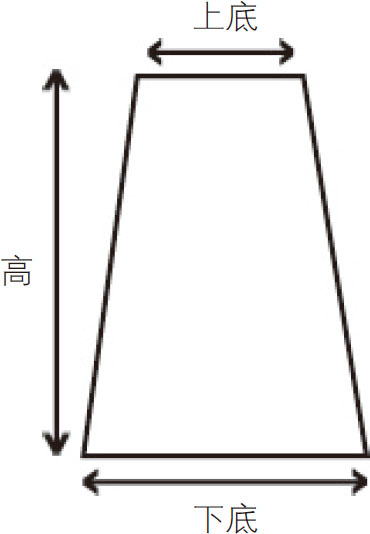
梯形：

面积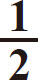＝×高（下底＋上底）

（面积＝［底1＋底2］×垂直高度×）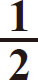

■立体几何图形表面积和体积的计算公式：

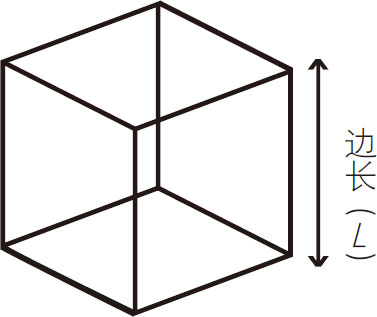
立方体：

表面积＝6L²（6×1条边长的平方）

体积＝L³（1条边长的立方）

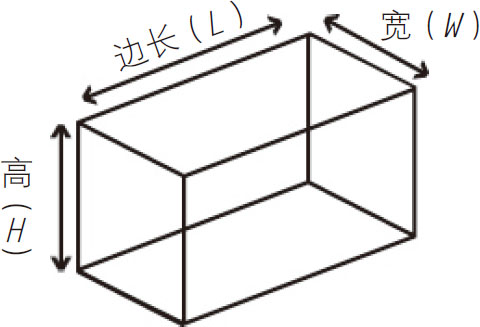
长方体：

表面积＝2（LH＋LW＋HW）

体积＝长×宽×高

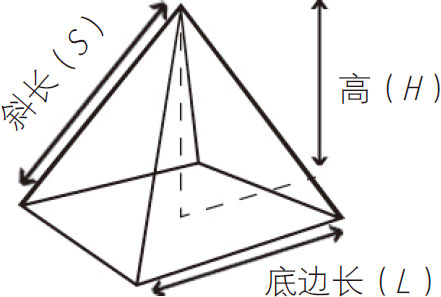
方形金字塔：

表面积＝2HS＋L²

体积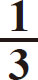＝L² H

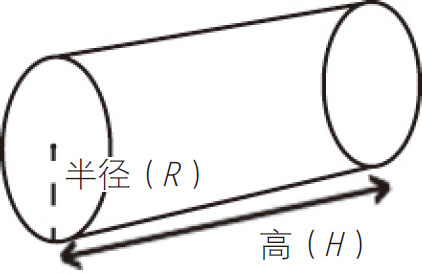
圆柱体：

表面积＝2πR²＋2πRH 体积＝πR²H

(www.xing528.com)

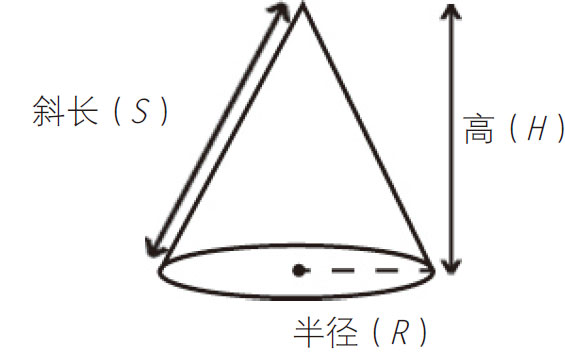
圆锥体

表面积＝πRS＋πR²

体积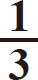＝πR²H

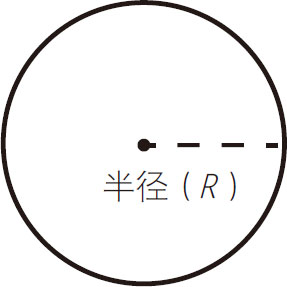
球（体）：

表面积＝4πR²

体积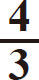＝πR³

实验8 欧拉多面体公式演示

瑞士数学家莱昂哈德·欧拉发现了扁平无曲线的平边几何图形的共同特征——它们都遵循这一公式：

V–E＋F＝2

V＝顶点数

（这是多边的交汇点）

E＝边数

F＝面数

（它是边的表面积）

无论一个多面体的形状是什么样，公式的结果总是2（除了计算机生成的特殊形状），见图3-1。

图3-1

图3-2是一个四面体，它有4个顶点、6条边、4个面。计算的结果是：

4–6＋4＝2

图3-3、图3-4、图3-5分别展示了不同形状的多面体，它们都遵循欧拉多面体公式。

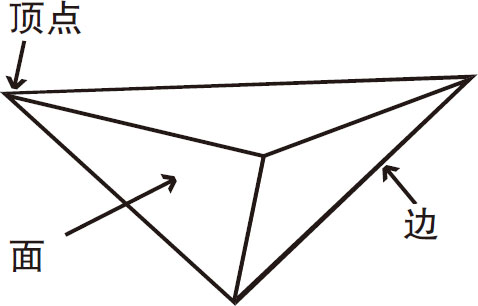
图3-2

V–E＋F＝2

4–6＋4＝2

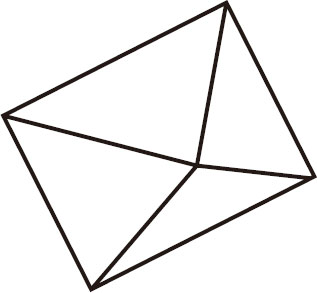
图3-3

V–E＋F＝2

5–8＋5＝2

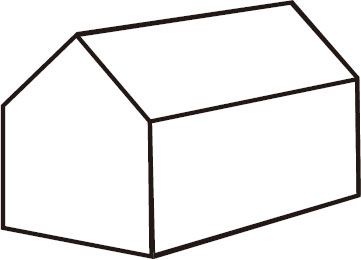
图3-4

V–E＋F＝2

10–15＋7＝2

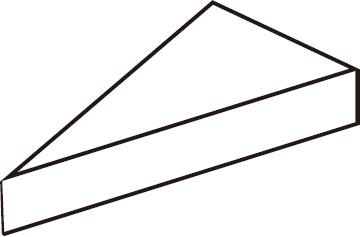
图3-5

V–E＋F＝2

6–9＋5＝2

-3＋5＝2

你可以用一块奶酪来演示欧拉多面体公式。

需要准备的东西：

►奶酪块

►小刀

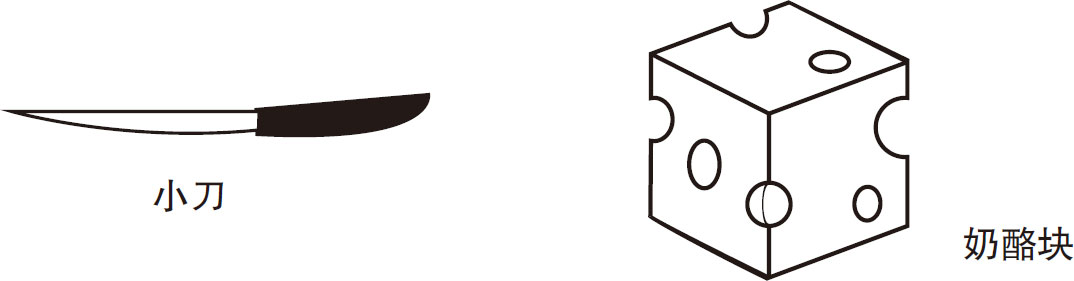
沿着奶酪块对角线的方向切去一端，见图3-6。

图3-6

计算剩余的顶点、边、面，用欧拉多面体公式写出你的结果。

不断地从奶酪块上沿对角线切下一部分，你会发现每次剩下的多面体都会遵循这个公式，见图3-7、图3-8、图3-9、图3-10。

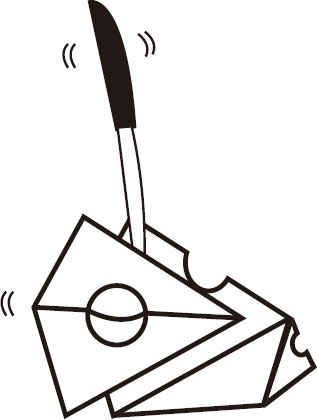
图3-7

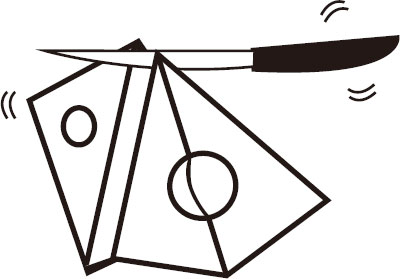
图3-8

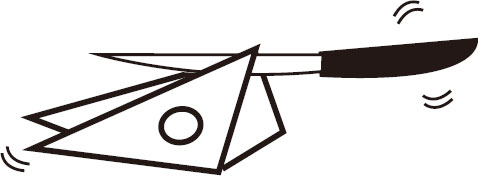
图3-9

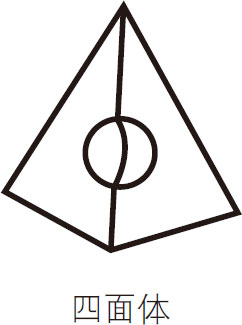
图3-10