典型方程法在结构力学中的应用

以上以一个简单例子讨论了位移法的基本原理。为了加深对位移法的理解，下面再以一个有侧移刚架的例子，进一步说明位移法的典型方程和解题步骤。

如图8-15所示刚架，13杆和24杆有侧移产生，这种结构称为有侧移结构。此刚架有一个独立结点角位移Z1和一个独立结点线位移Z2，共有两个基本未知量。在结点1处加一刚臂，结点2处加一水平支承链杆，得到基本结构。令其附加刚臂发生与原结构相同的转角Z1，同时令附加链杆发生与结构相同的线位移Z2，使得到基本体系。按类似前面例子的思路分析可知，基本体系的变形和内力与原结构完全相同，所以基本结构在结点位移Z1，Z2和荷载F共同作用下，刚臂上的附加反力矩和链杆上的附加反力R2都应等于零。设由Z1，Z2和F所引起的刚臂上的反力矩分别为R11，R12和R1P，所引起链杆上的附加反力分别为R21，R22和R2P，如图8-15（c）（d）（e）所示，则根据叠加原理可得

R1=R11+R12+R1P=0

R2=R21+R22+R2P=0

图8-15

再设以r11，r12分别表示由单位和所引起的刚臂上的反力矩，以r21，r22分别表示由单位位移和所引起的链杆上的反力，则上式可写为

该方程称为位移法典型方程，它的物理意义是：基本结构在荷载等外因和各结点位移的共同作用下，每一个附加联系上的附加反力矩和附加反力都应等于零。因此，它实质上是反映了原结构的静力平衡条件。

对于具有n个独立结点位移的结构，相应的在基本结构中需加入n个附加联系，根据每个附加联系的附加反力矩或附加反力均应为零的平衡条件，同样可建立n个方程如下：

在上述典型方程中，主斜线上的系数rii称为主系数或主反力；其他系数rij称为副系数或副反力；RiP称为自由项。系数和自由项的符号规定是：以与该附加联系所设位移方向一致者为正。主反力rii的方向总是与所设位移Zi的方向一致，故恒为正，且不会为零；副系数和自由项则可能为正、负或零。此外，根据反力互等定理可知主斜线两边处于对称位置的两个副系数rij与rji的数值是相等的，即rij=rji。

由于在位移法典型方程中，每个系数都是单位位移所引起的附加联系的反力（或反力矩）。显然，结构的刚度愈大，这些反力（或反力矩）也愈大，故这些系数又称为结构的刚度系数，位移法典型方程又称为结构的刚度方程，位移法也称为刚度法。

为了求出典型方程中的系数和自由项，可借助于表8-1，绘出基本结构在和以及荷载作用下的弯矩图和M图，如图8-16（a）（b）（c）所示。然后，由平衡条件求出各系数和自由项。

系数和自由项可分为两类：一类是附加刚臂上的反力矩r11，r12和R1P；另一类是附加链杆上的反力r21，r22和R2P。对于刚臂上的反力矩，可分别在图8-16（a）（b）（c）中取结点1为隔离体，由力矩平衡方程ΣM1=0求得为

对于附加链杆上的反力，可以分别为图8-16（a）（b）（c）中用截面割断两柱顶端，取柱顶端以上横梁部分为隔离体，并由表8-1查出竖柱13、24的杆端剪力，由投影方程求得为

图8-16

将系数和自由项代入典型方程（8-4）有

解得

所得均为正值，说明Z1，Z2所设方向相同。

结构的最后弯矩图可由叠加法绘制：

例如，杆端弯矩M31之值为

其他各杆端弯矩可同样算得，M图如图8-17所示。求出M图后，F图、FN图即可由平衡条件得出。

图8-17

对最后内力图应进行校核，包括平衡条件的校核和位移条件的校核。校核的方法与力法中所述一样，不再重复。

（1）确定原结构的基本未知量，即独立的结点角位移和线位移数目，加入附加联系而得到基本结构。

（2）令各附加联系发生与原结构相同的结点位移，根据基本结构在荷载等外因和各结点位移共同作用下，各附加联系上的反力矩或反力均应等于零的条件，建立位移法的典型方程。绘出基本结构在各单位结点作用下的弯矩图和荷载作用下（或支座位移、温度变化等其他外因作用下）的弯矩图，由平衡条件求出各系数和自由项。(www.xing528.com)

（3）解典型方程，求出作为基本未知量的各结点位移。

（4）按叠加法绘制最后的弯矩图。

可以看出，位移法和力法在计算步骤上是极为相似的，但二者的原理却有所不同，读者可自行一一对比，分析二者的区别及联系，以加深理解。

【例8-1】试用位移法求图8-18（a）所示阶梯形变截面梁的弯矩图。E为常数。

图8-18

【解】

此结构的基本未知量为结点B的角位移Z1和竖向位移Z2，基本结构如图8-18（b）所示。

根据基本结构在荷载和Z1，Z2共同作用下，附加刚臂上反力矩和附加链杆上反力等于零的条件，建立位移法典型方程如下：

r11Z1+r12Z2+R1P=0

r21Z1+r22Z2+R2P=0

设i=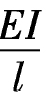，则iAB=3i，iBC=i。绘出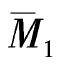图和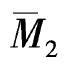图和MP图，如图8-18（c）（d）（e）所示，然后取结点B处的隔离体，利用力矩和竖向投影平衡条件可求出系数和自由项：

R1P=0，R2P=-F

代入典型方程得

解得

由叠加原理M=Z1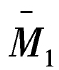+Z2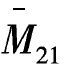+MP可得最后弯矩图，如图8-18（f）所示。

【例8-2】图8-19（a）所示刚架的支座A产生转角φ，支座B产生竖向位移Δ=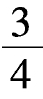lφ。试用位移法绘其弯矩图。E为常数。

图8-19

【解】

此刚架的基本未知量只有结点C的角位移Z1，在结点C加一附加刚臂即得基本结构，相应的位移法典型方程为

r11Z1+R1Δ=0

设i=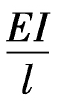，则iAC=i，iBC=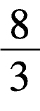i。如图8-19（c）（d）所示，绘出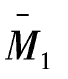图和MΔ图后可求得

于是，可解出基本未知量

刚架的最后弯矩图可由M=Z1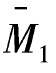+MΔ绘出，如图8-19（e）所示。