结构力学中支座移动的力法计算

支座移动下力法计算的原理、方法、步骤同荷载及温度作用下一样。基本未知量与基本系的选择原则、方法，不因结构受外界因素的变化而改变。图7-20（a）为三次超静定结构，B支座下沉了VB=a，向右移了UB=b，顺时针方向转动了θB=φ。选择基本系，力法典型方程为

式中，Δ1C，Δ2C，Δ2C为支座移动在基本系上解除约束处引起的位移。

图7-20

若基本系取图7-20（b）的形式，根据第六章中支座移动下位移计算公式

需计算多余约束力作用下在有支座移动处的支座反力

当时，如图7-20（d）所示，

C1=a，C2=b，C3=c

则

Δ1C=-（0×a+1×b+h×φ）=-b-hφ

当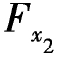=1时，如图7-20（e）所示，

则

当Fx3=1时，如图7-18（f）所示，

则

Δ3C=-（0×a+0×b+（-1）×φ）=φ

系数之求解同前。系数求出后，连同自由项一起代入典型方程，求出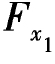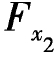，，Fx3。

若基本系取图7-20（c），在支座移动处解除约束，这时Δ1C，Δ2C，Δ3C的计算仍然可用公式（请读者自己求）。如果求解的问题比较简单，也用几何直观来求。如Δ1C是由于支座移动而在基本系上解除约束方向的位移，这位移仅由VB=a引起，且与方向一致，而UB和θB均不引起方向的位移；Δ2C是由于支座移动而在基本系上方向的相对位移，也仅是由UB=b引起的，方向与相反；Δ3C也同样仅是由θB引起的，但方向相反。所以

Δ1C=a，Δ2C=-b，Δ3C=φ

两种基本系的自由项不同，系数也不同，解出的基本未知量也不同，但结构的最后内力是一样的。

【例7-6】作图7-21所示结构在温度改变和支座移动因素共同作用下的弯矩图。

图7-21

【解】

这是一次超静定结构，选基本系为简支刚架形式较方便，如图7-22（a）所示。

（1）温度改变作用。(www.xing528.com)

温度改变作用需考虑弯矩项与轴力项，绘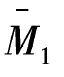与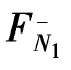图，如图7-22（b）（c）所示，则

杆AB和杆CD：

t2-t1=0，故Δ1t中第一项为零；因杆无轴力，所以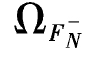=0，则第二项也为零。

杆BC：

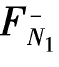=-1，所以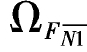=（-1）×10m=-10m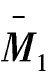；=6m，所以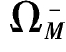=6m×10m=60m2。杆BC是上侧受拉，按温度与变形一致的原则，设受拉一面温度升高为t2，则

于是由温度改变引起的位移Δ1t为

将系数与自由项代入典型方程δ11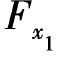+Δ1t=0，得

解得　Fx1=-4.475×10-5EI0

最后由温度改变引起的弯矩为

把EI0数值代入后，杆端弯矩为

MBA=MBC=MCB=MCD=5.37kN·m

由温度改变引起的弯矩图如图7-22（d）所示。从最后杆端弯矩的表达式可以看出：温度改变引起的自内力与刚度绝对值成正比。所以，工程中若要减小温度应力，则不能采取加大断面的办法。

图7-22

（2）支座移动作用。

基本系仍选图7-22（a），主系数δ11与前相同，由几何关系得自由项Δ1C=0.02m。由公式计算时要注意支座反力方向应假设成与支座位移方向一致，则

于是

支座移动不引起基本系（静定结构）的内力，故最后弯矩图如图7-22（f）所示，表达式为

从杆端弯矩的表达式（如MBA=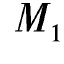×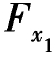=-37.0kN·m）可看出，支座移动引起的弯矩与抗弯刚度绝对值成正比。刚度越大，支座移动引起的内力越大。上例中支座只移动20mm，杆端弯矩便有37.0kN·m的数值。这就是工程上为什么要十分关心不均匀沉陷的问题所在。

最后还要强调指出，结构在外荷载作用下，它的内力与各杆件之间刚度的相对比值有关，而与绝对值无关，但结构在温度改变与支座移动作用下，由于系数与刚度有关，而自由项与刚度无关，所以最后的内力与刚度的绝对值有关。

随堂练习

如图7-23所示结构，当内外侧均升高t1℃时，两杆均只产生轴力。（　　）

图7-23