结构力学（上）：图乘法的应用及求解

从前节的例题计算中可看出，结构位移计算与结构内力计算有密切的关系。内力计算时列内力方程，对应的位移计算方法称为积分法。

在位移计算中，如属两种情况：①匀质等截面直杆段，即EI，EA，GA均为常量，杆轴线为直线；②位移状态与平衡状态相对应的内力图中有一图形是直线变化的；则可把结构位移计算的积分法换成图形相乘的方法，即利用内力图进行运算，使计算简化。

设有匀质等截面直杆段AB的内力图，如图6-21所示，两内力图中一图为直线变化，如图。现以杆轴线AB为x轴，它与的夹角为α，由图得=xtanα。因EI=常数，则积分的位移公式为

图6-21

积分号内表示MP图的面积（MPdx）对y轴的矩。若用ΩAB代表MP图的面积，用xC代表MP图形心C的横坐标，用yC代表MP图形心C所对应的直线图形（图）的纵坐标，则上式可写为

式中，ΩAB表示曲线图形的面积；yC表示曲线图形形心所对应的直线图形的竖标。

由上述假设，剪力项与轴力项也同样可得如下结果：

荷载作用下，位移的计算公式可改写为

应用上述图乘法时应注意下列几点：

（1）面积Ω应取曲线的图形，坐标yC取直线图形，且是Ω的形心所对应的竖标值。

（2）当两个内力图都在杆轴同一侧（对剪力图和轴力图应为同符号）时，相乘结果为正号，异侧时（对剪力图和轴力图为异号）相乘结果取负号。

（3）两图形相乘后还要除以杆段的刚度。

（4）如图6-22所示，若直线图形是由若干直线段组成的，则相乘时要分段图乘，即

图6-22

（5）复杂图形要分解成几个简单的几何图形，以便利用常用的面积和形心公式进行计算。

图6-23给出了位移计算中几种常见图形的面积和形心的位置。在应用抛物线图形公式时，要注意抛物线在顶点处的切线必须与基线平行。

图6-23

图6-24给出了几种简单图形相乘的结果，建议读者自行证明并予以熟记，这对今后的运算是有帮助的。对于比较复杂的图形，应将图形分解成几个较简单的图形，分别图乘后叠加，如图6-24（g）（h）（i）（j）所示。

图6-24

【例6-4】用图乘法校核例6-3用积分法计算所得的结果。已知EI=常数。

图6-25

【解】

（1）建立平衡状态，如图6-25（c）所示。

（2）作MP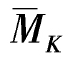，图，如图6-25（b），图6-25（d）所示。

（3）用图乘法计算跨中挠度。

MP图是由两段直线组成的，是对称的，故图乘时要分为两段。由于MP是直线图形，取竖标yC，MP图为曲线图形，计算中取面积Ω。

与用积分法计算的结果完全相同。

【例6-5】悬臂梁AB段的截面惯矩为I1，BC段的截面惯矩为I2，受匀布荷载q作用，如图6-26（a）所示，求自由端的挠度。设I2=2I1，略去剪力的影响。

【解】

（1）建立静力状态，如图6-26（c）所示。

（2）作MP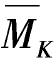，图，如图6-26（b）和图6-26（d）所示。

（3）用图乘法求位移。(www.xing528.com)

略去微小段牛腿的影响，得一阶梯形的变截面梁。由于上下两段的截面惯矩不同，所以分两段图乘。

AB段：因MP图为二次抛物线，利用标准二次抛物线与三角形相图乘，得

图6-26

BC段：BC段的曲线图形在B点不符合切点的条件，这时可把B点与C点的竖标连以直线，使原来曲线的图形增加一块抛物线的面积，成为梯形面积如图6-26（e）所示。当MP与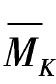两图相乘时，先用两梯形面积相图乘后再减去增加的抛物线图形与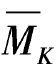图相乘的数值。计算如下

两段相加，得

若I1=4I2，则

【例6-6】求图6-27（a）所示刚架C点的水平线位移ΔCP。已知柱AB和梁BC的截面惯性矩分别为I和1.2I。

【解】

（1）建立平衡状态，如图6-27（b）所示。

（2）作MP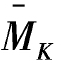，图，如图6-27（c）和图6-27（d）所示。

图6-27

（3）用图乘法求位移ΔCP。

图乘时在MP图中取面积Ω，在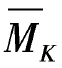图中取纵距yC。柱AB的图形用虚线分为一个直角三角形ABb（Ω1）和一个抛物线图形Aeb（Ω2），梁BC段的图形用虚线分为直角三角形Bb'C（Ω3）和三角形b'Cd（Ω4）。分别求Ω和y。

负号表示C点位移方向与原设相反，实际应是向左的。

【例6-7】设有一矩形钢筋混凝土渡槽，如图6-28（a）所示，槽身的计算简图如图6-28（b）所示，试求槽内最高水位时A，B两点的相对水平线位移。已知EI=2.1×107kN/m2×2.81×10-3m4=5.901×104kN·m2，γ水≈10kN/m（3设结构自重不计，并略去轴力及剪力对位移的影响）。

图6-28

【解】

（1）建立平衡状态。对应于相对水平线位移，在A，B两点的水平方向虚设一对等量、反向的单位集中力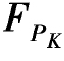=1，如图6-2（8c）所示。

（2）作内力图MP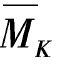，，如图6-28（d）、图6-28（e）所示。

（3）用图乘法计算位移。

MP图为曲线变化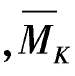图为直线变化。图乘时，面积Ω取自MP，纵距yC取自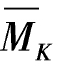图。

杆AC及杆BD：

杆CD：

所得结果为正，说明位移与假设方向一致，两点是相互分开的，位移图如图6-28（f）所示。

随堂练习

1.在图乘法中，欲求某点的转角，则应在该点虚设（　　）。

A.竖向单位力　B.水平向单位力

C.任意方向单位力　D.单位力偶

2.在图乘法中，欲求某点的竖向位移，则应在该点虚设（　　）。

A.竖向单位力　B.水平向单位力

C.任意方向单位力　D.单位力偶