三铰拱支座反力：结构力学（上）

三铰拱是由法国和德国工程师在19世纪中期开发的结构形式。1889年巴黎博览会著名的机械厅（Palaisdes Machines）就是由一系列三铰拱组成的。三铰拱与三铰刚架的几何组成形式相同，都属于三刚片结构，其支座反力、截面内力的计算方法也是相同的，即需要利用整体平衡和局部平衡联立求解。

下面以竖向荷载作用下的平拱（图4-5a）为例，说明三铰拱支座反力和内力的计算方法。为了使概念清晰、便于计算，这里将与三铰拱跨度相同、竖向荷载也相同的简支梁称为相应简支梁或代梁（图4-5b），将二者受力情况加以对比，找出联系。

图4-5

考虑图4-5（a）所示三铰拱的整体平衡，求得两个竖向支座反力并建立两个水平反力之间的关系

其中，式（4-3）中的FH称为推力。

再取顶铰C任一侧半拱为隔离体计算水平反力。若取AC为隔离体，由以C点为矩心的平衡条件可得

将式（4-1）和式（4-2）与相应简支梁的两个竖向反力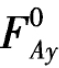和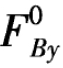进行比较，再将式（4-4）右端项分子与相应简支梁上同拱的顶铰对应的截面C的弯矩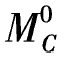加以比较，可以得到

式（4-5）表明三铰拱的支座反力具有如下特点：(www.xing528.com)

（1）所有反力与拱轴线形状无关，只取决于荷载与三个铰A，B，C的相对位置。

（2）在竖向荷载作用下，三铰平拱的竖向支座反力等于相应简支梁对应的竖向支座反力，与拱高无关；两个水平反力等值反向，等于相应简支梁截面C的弯矩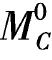除以拱高f；荷载竖直向下时，水平反力指向三铰拱的内侧（故称推力）。

（3）当荷载与拱的跨度不变时，水平推力FH与拱高f成反比，即f越小，拱越平坦，FH越大。当f→0时，FH→∞，此时三个铰在一条直线上，拱成为几何瞬变体系。在工程实际中，拱结构的高跨比f/l一般为1/10～1。

以上求解的是平拱（两拱趾等高）的计算。三铰斜拱支座反力的求解与不等高三铰刚架的求解类似，可由整体的力矩平衡ΣMB=0及左半个拱AC的力矩平衡ΣMC=0联立解方程，求解出支座反力FAy和FH，然后由整体的ΣMA=0求出FBy。

随堂练习

判断图4-6所示两个三铰拱支座反力是否相同？

图4-6