计算机中数据的转换过程

二进制只有“0”和“1”两个数，相对十进制而言，采用二进制表示不但运算简单、易于物理实现、通用性强，更重要的优点是所占用的空间和所消耗的能量小得多，而且其可靠性大大提高。计算机内部均用二进制数表示各种信息，但计算机与外部交往仍采用人们熟悉和便于阅读的形式，如十进制数据，文字显示和图形描述等。期间的转换，则由计算机系统的硬件和软件来实现，转换过程如图1-2所示。

用若干数位（由数码表示）的组合去表示一个数，各个数位之间是什么关系，即逢“几”进位，这就是进位计数制的问题，也就是数制问题。数制，即进位计数制，是利用数字符号按进位原则进行数据大小计算的方法，通常是以十进制来进行计算的。另外，还有二进制、八进制和十六进制等。

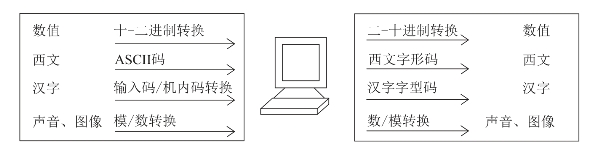
图1-2　各类数据在计算机中的转换过程

1.十进制（D）

十进制的特点如下：

（1）有10个数码：0、1、2、3、4、5、6、7、8、9。

（2）基数：10。

（3）逢十进一（加法运算），借一当十（减法运算）。

（4）按权展开式。对于任意一个n位整数和m位小数的十进制数D，均可按权展开为

D=Dn-1·10n-1+Dn-2·10n-2+…+D1·101+D0·100+D-1·10-1+…+D-m·10-m

例　将十进制数456.24写成按权展开式形式为

456.24=4×102+5×101+6×100+2×10-1+4×10-2

2.二进制（B）

二进制的特点如下：

（1）有两个数码：0、1。

（2）基数：2。

（3）逢二进一（加法运算），借一当二（减法运算）。

（4）按权展开式。对于任意一个n位整数和m位小数的二进制数D，均可按权展开为

D=Bn-1·2n-1+Bn-2·2n-2+…+B1·21+B0·20+B-1·2-1+…+B-m·2-m

例　把（11001.101）2写成展开式，它表示的十进制数为

1×24+1×23+0×22+0×21+1×20+1×2-1+0×2-2+1×2-3=（25.625）10

3.八进制（O）(www.xing528.com)

八进制的特点如下：

（1）有8个数码：0、1、2、3、4、5、6、7。

（2）基数：8。

（3）逢八进一（加法运算），借一当八（减法运算）。

（4）按权展开式。对于任意一个n位整数和m位小数的八进制数D，均可按权展开为

D=On-1·8n-1+…+O1·81+O0·80+O-1·8-1+…+O-m·8-m

例　（5 346）8相当于十进制数为

5×83+3×82+4×81+6×80=（2 790）10

4.十六进制（H）

十六进制的特点如下：

（1）有16个数码：0、1、2、3、4、5、6、7、8、9、A、B、C、D、E、F。

（2）基数：16。

（3）逢十六进一（加法运算），借一当十六（减法运算）。

（4）按权展开式。对于任意一n位整数和m位小数的十六进制数D，均可按权展开为

D=Hn-1·16n-1+…+H1·161+H0·160+H-1·16-1+…+H-m·16-m

在16个数码中，A、B、C、D、E和F这6个数码分别代表十进制的10、11、12、13、14和15，这是国际上通用的表示法。

例　十六进制数（4C4D）16代表的十进制数为

4×163+C×162+4×161+D×160=（19 533）10

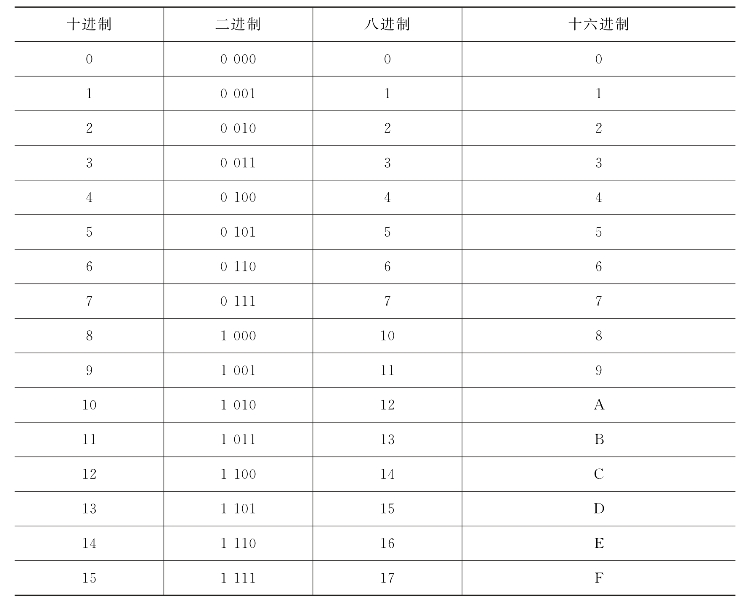
二进制数与其他数之间的对应关系如表1-2所示。

表1-2　几种常用进制之间的对照关系