2006年全国硕士研究生入学统一考试数学试题解析

一、填空题

（1）分析 只要计算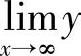，即能得到水平渐近线方程.

精解 由于，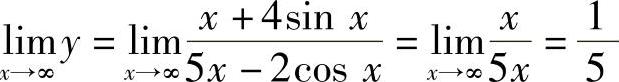

所以，所给曲线的水平渐近线方程为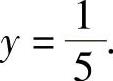

附注 在计算曲线y=y（x）的水平渐近线方程时，如果不存在，则应分别计算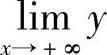和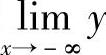，当它们的极限值分别为A，B时，则有渐近线y=A和y=B.

（2）分析 利用函数f（x）在点x=0处连续即可算得a的值.

精解 由于f（x）在点x=0处连续，所以

附注 分段函数中包含的未知常数，往往利用分段点处连续或可导的条件来确定.

（3）分析 利用变量代换法将反常积分转换成定积分后计算.

精解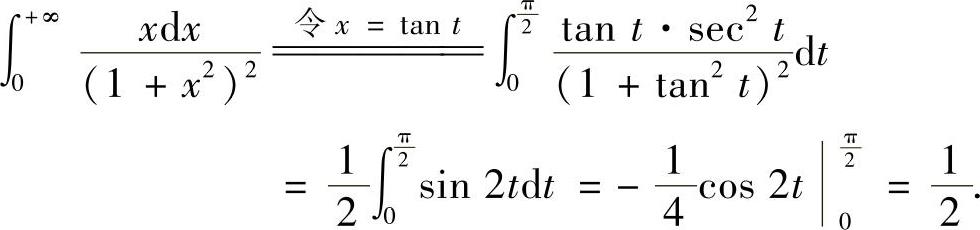

附注 由于所给反常积分是收敛的，故也可以如计算定积分那样计算：

（4）分析 所给微分方程是变量可分离的微分方程.

精解 所给微分方程可改写为

两边积分得

lny=lnx-x+lnC.

所以，所给微分方程的通解为y=Cxe^-x.

附注 要熟练掌握四类一阶微分方程（变量可分离的微分方程、齐次微分方程、一阶线性微分方程（包括伯努利方程）和全微分方程）的求解方法.

（5）分析 先计算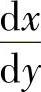，由此得到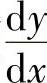，然后将x=0代入得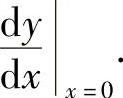

精解 所给方程可以改写为x=（1-y）e^-y，所以

由此得到

于是

附注 本题也可以先按定义直接算出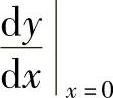，具体计算如下：

（6）分析 按公式|MN|=|M|·|N|（其中M，N都是n阶矩阵）计算.

精解 所给等式可以改写成

B（A-E）=2E.

所以|B||A-E|=4，其中

因此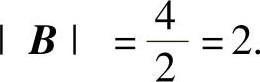

附注 关于n阶矩阵的行列式有以下性质（应熟记）：

设A，B都是n阶矩阵，则

（ⅰ）|kA|=kⁿ|A|（k为常数）.

（ⅱ）|A^T|=|A|.

（ⅲ）|AB|=|A||B|.

（ⅳ）设A是可逆矩阵，则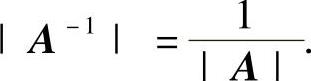

（ⅴ）当n≥2时，|A^∗|=|A|^n-1.

（ⅵ），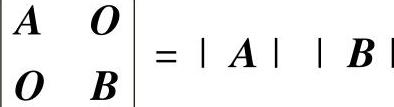

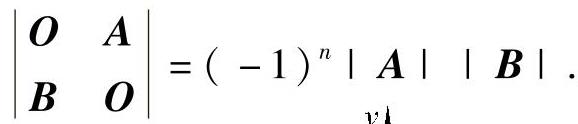
二、选择题

（7）分析 画出y=f（x）的概图，然后按Δy，dy的几何表示选择正确选项.

精解 由f′（x）＞0和f″（x）＞0可得函数y=f（x）的概图如图B-06-1所示，其中MT是曲线y=f（x）在点M（x₀，f（x₀））处的切线，于是当Δx＞0时，

由图可知，0＜dy＜Δy.

因此本题选（A）.

图 B-06-1

附注 本题是利用Δy与dy的几何解释获解的，也可以用分析方法求解，具体如下：当Δx＞0时，有

Δy=f（x₀+Δx）-f（x₀）=f′（ξ）Δx （其中ξ∈（x₀，x₀+Δx））

＞f′（x₀）Δx（由于f″（x）＞0）

=dy＞0（由于f′（x₀）＞0）.

（8）分析 利用积分上限函数的性质确定正确选项.

精解 由于f（x）是奇函数，所以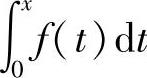是偶函数.

由于f（x）除第一类间断点x=0外，处处连续，所以f（x）是可积函数，从而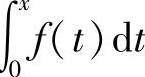连续.

因此本题选（B）.

附注 应记住积分上限函数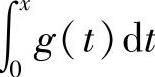的以下性质：

（ⅰ）如果g（x）可积，则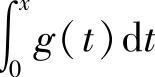连续.

（ⅱ）如果g（x）连续，则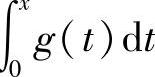可导，且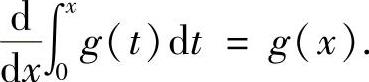

（ⅲ）如果g（x）是奇函数，则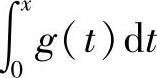是偶函数；如果g（x）是偶函数，则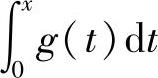是奇函数.

（ⅳ）如果g（x）是以T为周期的周期函数，且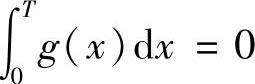，则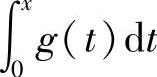是以T为周期的周期函数.

（9）分析 计算h（x）的导数，并将h′（1），g′（1）的值代入即得g（1）.

精解 由g（x）可微知h（x）=e^1+g（x）可微，且

h′（x）=e^1+g（x）·g′（x）.上式中令x=1，则由h′（1）=1，g′（1）=2得

1=e^1+g（1）·2，即g（1）=-ln2-1.

因此本题选（C）.

附注 由于题设中有h′（1）=1，g′（1）=2，所以很自然地要通过求导计算g（1）的值.

（10）分析 由y=C₁e^x+C₂e^-2x+xe^x知对应的常系数齐次线性微分方程的特征方程应有特征根为r=1，-2.由此排除两个选项.再将xe^x代入常系数非齐次线性微分方程，即可确定正确选项.

精解 由y=C₁e^x+C₂e^-2x+xe^x知，C₁e^x+C₂e^-2x是对应的常系数齐次线性微分方程的通解，所以该齐次线性微分方程的特征方程有根r=1，-2，即特征方程为

r²+r-2=0，从而该齐次线性微分方程为y″+y′-2y=0.故排除选项（A）、（B）.

将xe^x代入y″+y′-2y得

（x+2）e^x+（x+1）e^x-2xe^x=3e^x，

即xe^x是选项（D）的微分方程的一个特解.

因此本题选（D）.

附注 由本题的题解可知，先根据对应的齐次线性微分方程的通解排除两个不正确的选项（A）、（B），然后根据非齐次线性微分方程的特解确定正确选项.

（11）分析 按所给的二次积分画出对应的二重积分的积分区域，然后写出对应的关于“先x后y”或“先y后x”的二次积分.

精解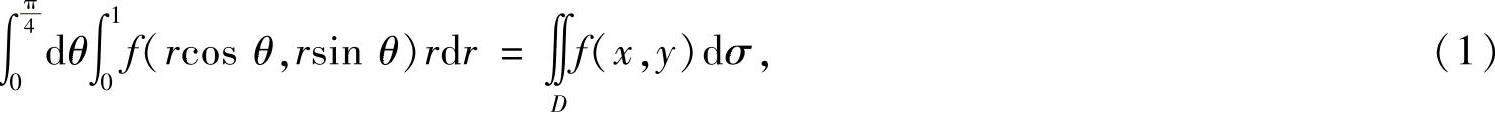

其中D={（x，y）|x²+y²≤1，0≤y≤x}，如图B-06-2阴影部分所示.

对式（1）的二重积分采用“先x后y”方法积分得

将式（2）代入式（1）得

因此本题选（C）.

附注 设f（x，y）是连续函数，要更换关于它的二次积分的积分次序或更换关于它的二次积分的坐标系，重要的是确定相对应的二重积分的积分区域D.

例如，要将本题的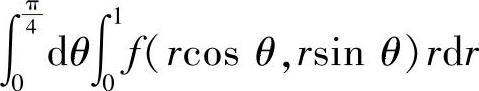转换成“先y后x”的二次积分，则需将D划分成D₁与D₂（图B-06-2），其中

图 B-06-2

于是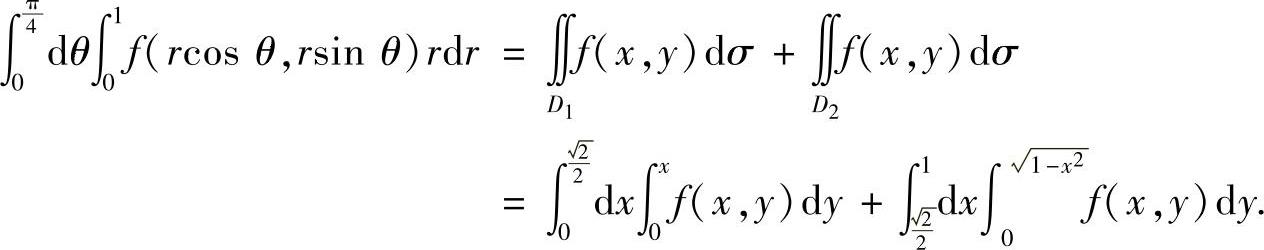

（12）分析 用二元函数条件极值的拉格朗日乘数法判定正确选项.

精解f（x，y）在约束条件φ（x，y）=0下的极值点可用拉格朗日乘数法求解.故作拉格朗日函数

F（x，y）=f（x，y）+λφ（x，y），

则（x₀，y₀）满足

其中λ₀是对应（x₀，y₀）的λ值.消去其中的λ₀得

f′_x（x₀，y₀）φ_y′（x₀，y₀）-f_y′（x₀，y₀）φ_x′（x₀，y₀）=0.

由此可知，当f_x′（x₀，y₀）≠0时，由于φ_y′（x₀，y₀）≠0，必有f_y′（x₀，y₀）≠0.

因此本题选（D）.

附注 设f（x，y），φ（x，y）都是可微函数，则f（x，y）在约束条件φ（x，y）=0下的极值点（x₀，y₀）满足方程组

但满足上述方程组的点（x₀，y₀）未必是f（x，y）在约束条件φ（x，y）=0下的极值点，只是可能极值点.

（13）分析 由于α₁，α₂，…，α_s是抽象的向量组，所以其线性相关性的判定应从定义入手.

精解 先考虑选项（A）的正确性.

由α₁，α₂，…，α_s线性相关知，存在一组不全为零的数k₁，k₂，…，k_s，使得

k₁α₁+k₂α₂ +…+k_sα_s=0.

从而存在一组不全为零的数k₁，k₂，…，k_s使得k₁Aα₁+k₂Aα₂+…+k_sAα_s=A（k₁α₁+k₂α₂+…+k_sα_s）=A0=0，所以Aα₁，Aα₂，…，Aα_s线性相关.

因此本题选（A）.

附注 这里顺便指出，当α₁，α₂，…，α_s线性无关时，Aα₁，Aα₂，…，Aα_s未必线性无关，也未必线性相关，即Aα₁，Aα₂，…，Aα_s的线性相关性与A有关.

（14）分析 写出初等变换对应的初等矩阵即可.

精解 由题意得

（由于）.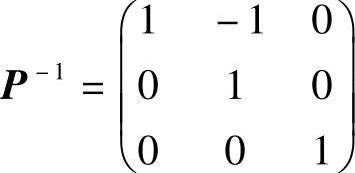

因此本题选（B）.

附注 应记住m×n矩阵A的每个初等变换对应的初等矩阵.

A的每个初等行变换所对应的初等矩阵是对m阶单位矩阵作相应的初等行变换而成的矩阵；A的每个初等列变换所对应的初等矩阵是对n阶单位矩阵作相应的初等列变换而成的矩阵.

每个n阶初等矩阵都是可逆矩阵，其逆矩阵是对n阶单位矩阵施行与此初等矩阵对应的初等变换的逆变换（例如，交换第i行与第j行的逆变换是交换第i行与第j行；第i行乘上不为零常数c的逆变换是第i行乘上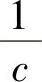；第i行乘以常数k加到第j行的逆变换是第i行乘以-k加到第j行.对初等列变换也有同样的说法）.

三、解答题

（15）分析 将e^x的带佩亚诺型余项的三阶麦克劳林公式代入所给等式后，比较x同次幂的系数，即可确定常数A，B，C的值.

精解 将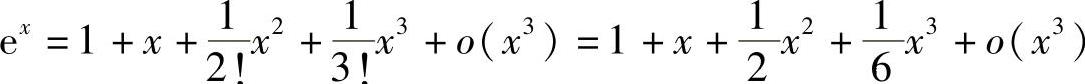代入

e^x（1+Bx+Cx²）=1+Ax+o（x³）

得 ，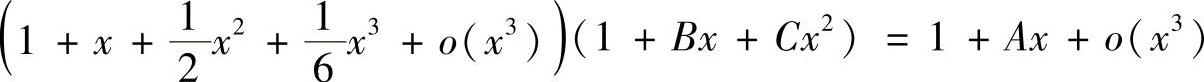

即

比较上式两边的x同次幂的系数得

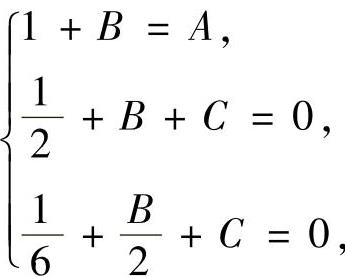即，，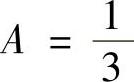

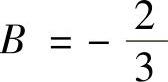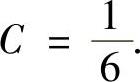
附注 本题也可以用洛必达法则计算，具体如下：

由所给等式得

连续应用洛必达法则得(www.xing528.com)

由式（1）知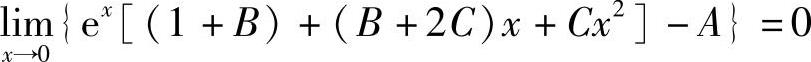，即1+B-A=0. （4）

由式（2）知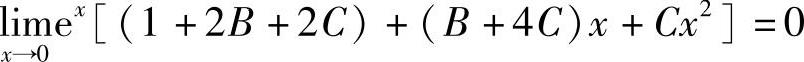，即1+2B+2C=0. （5）

由式（3）知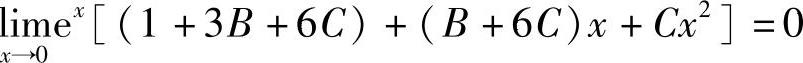，即1+3B+6C=0. （6）

由式（4）、式（5）和式（6）得，，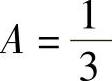

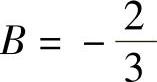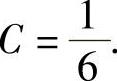
（16）分析 用分部积分法计算所给的不定积分.

精解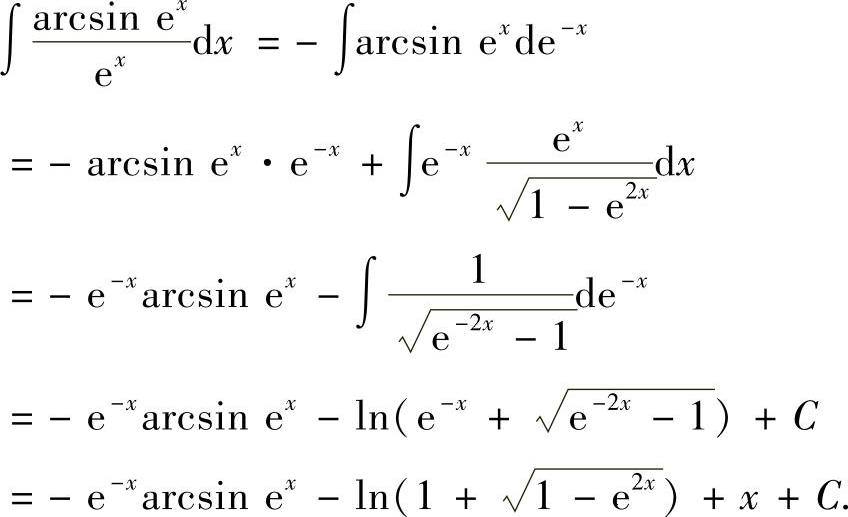

附注 本题也可综合应用换元积分法与分部积分法计算：

（17）分析 先利用积分区域的对称性化简I，然后用极坐标计算.

精解

附注 在计算二重积分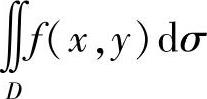时，首先应按积分区域D的对称性进行化简.常见的区域对称性有：

（ⅰ）D关于x轴（y轴）对称，则f（x，y）在对称点（x，y）与（x，-y）（（x，y）与（-x，y））处的值，互为相反数时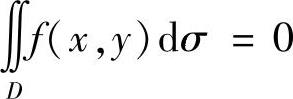，；彼此相等时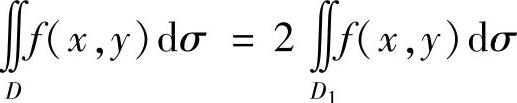，（其中D₁是按对称性将D划分成的两部分之一）.

（ⅱ）D关于原点对称（即既关于x轴对称，又关于y轴对称），则f（x，y）的值在对称点（x，y）与（-x，-y）处的值，互为相反数时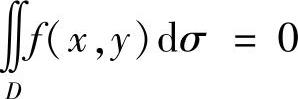，；彼此相等时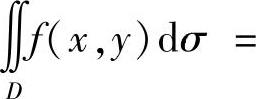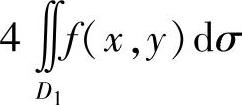，（D₁是按对称性将D划分成的四部分之一）.

（ⅲ）D关于直线y=x对称，则f（x，y）在对称点（x，y）与（y，x）处的值，互为相反数时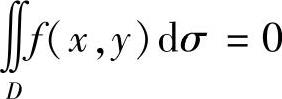，；彼此相等时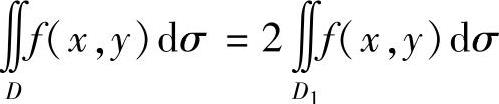，（D₁是按对称性将D划分成的两部分之一）.

本题的有关计算方法见提高篇12.

（18）分析 （Ⅰ）由于{x_n}是由递推式定义的，所以用数列极限存在准则Ⅱ确定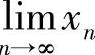存在，并求出该极限.

精解 （Ⅰ）当x∈（0，π）时，sinx＜x，所以对n=1，2，…有

0＜x_n+1=sinx_n＜x_n＜π，

即{x_n}单调减少有下界，所以由数列极限存在准则Ⅱ知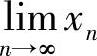存在，记其为a，则a∈[0，π）.令n→∞对递推式x_n+1=sinx_n两边取极限得a=sina.显然该方程在[0，π）内仅有解a=0.因此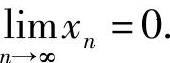

（Ⅱ）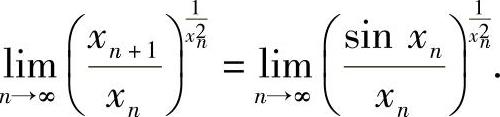

由于n→∞时，x_n→0，所以考虑极限

其中，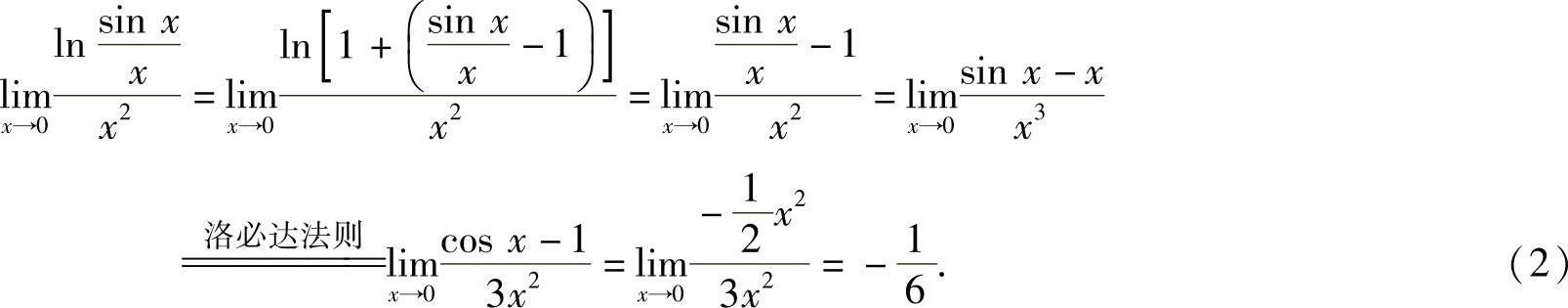

将式（2）代入式（1）得

因此，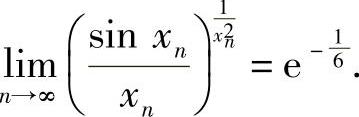

附注 对于1∞型未定式极限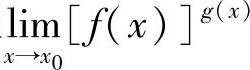（这里x₀可以为∞），除可直接应用重要公式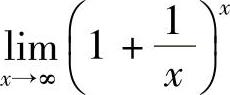或其推广形式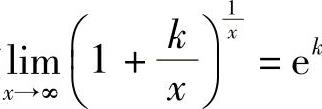外，其快捷计算步骤如下：

（ⅰ）由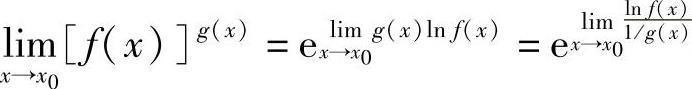将计算1^∞型未定式极限转换成计算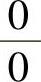型未定式极限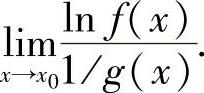

（ⅱ）使用重要极限公式、等价无穷小代替及洛必达法则计算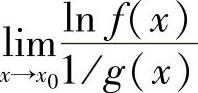，设其为A，则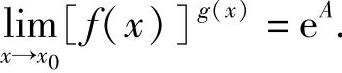

本题是综合题，其有关内容见提高篇01.

（19）分析 将b改为x，用导数方法证明函数不等式

xsinx+2cosx+πx＞asina+2cosa+πa （0＜a＜x≤b＜π）.

实际上，只要证明f（x）=xsinx+2cosx+πx在（0，π）上是单调增加的即可.

精解 由于f（x）在（0，π）上二阶可导且

f′（x）=sinx+xcosx-2sinx+π

=-sinx+xcosx+π，

f″（x）=-cosx+cosx-xsinx=-xsinx＜0，

所以，f′（x）在（0，π）上单调减少，故有

从而f（x）在（0，π）上单调增加，特别地，对0＜a＜b＜π有f（b）＞f（a），即

bsinb+2cosb+πb＞asina+2cosa+πa.

附注 题解中有两点值得注意：

（ⅰ）在证明文字不等式时，经常将其中的某个文字改为x，转换成函数不等式，然后用导数方法证明这个函数不等式.

（ⅱ）当辅助函数f（x）的导数f′（x）符号不易确定时，可考虑计算f″（x），通过它的符号确定f′（x）的符号.

本题的有关内容与证明方法见提高篇05.

（20）分析 （Ⅰ）对z求二阶偏导数，并将它们代入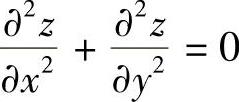即可证明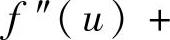

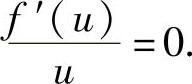
（Ⅱ）用降阶方法求解微分方程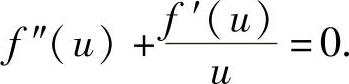

精解 （Ⅰ）记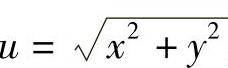，则

同样可得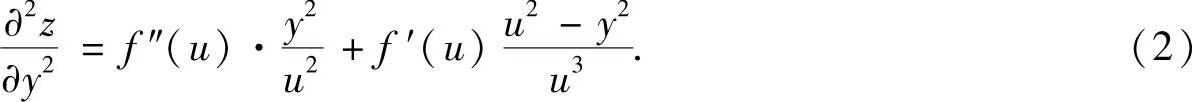

将式（1）、式（2）代入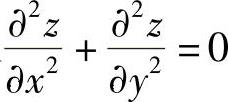得

（Ⅱ）式（3）可以改写成

uf″（u）+f′（u）=0，即[uf′（u）]′=0，

所以 uf′（u）=C₁.（4）

令u=1得C₁=f′（1）=1.代入式（4）得

uf′（u）=1，即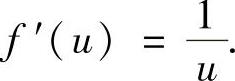

所以 f（u）=lnu+C₂.（5）

令u=1得C₂=f（1）=0.代入式（5）得

f（u）=lnu（u＞0）.

附注 微分方程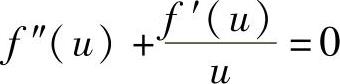也可以按如下方法求解：

记p=f′（u），则上述微分方程降阶为一阶线性微分方程

它的通解为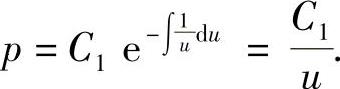将p|_u=1=f′（1）=1代入得C₁=1.所以有

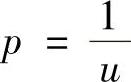，即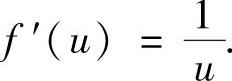

于是f（u）=lnu+C₂.将f（1）=0代入得C₂=0.因此f（u）=lnu（u＞0）.

本题是综合题，其有关内容与计算方法见提高篇10，14.

（21）分析 （Ⅰ）计算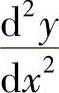即可确定L的凹凸性.

（Ⅱ）设对应切点的参数为t₀，则只要算出t₀即可得到切点和切线方程.

（Ⅲ）画出欲求面积的平面图形D，然后用积分计算D的面积.

精解 （Ⅰ）由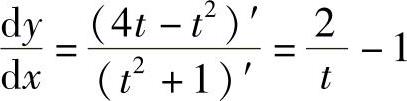得

所以，L是凸的.

（Ⅱ）设对应切点的参数为t₀，则切线方程为

即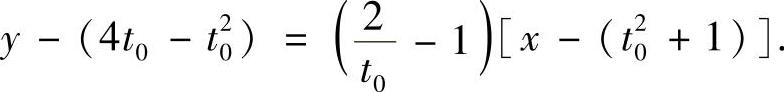

由于切线过点（-1，0），所以将x=-1，y=0代入式（1）得

化简得t²₀+t₀-2=0，即t₀=1，-2（不符合题意）.由此可知，

切点（x₀，y₀）=（2，3），切线方程为

y-3=x-2，即y=x+1.

（Ⅲ）欲求面积的平面图形如图B-06-3阴影部分所示，由图可知，D的面积

图 B-06-3

附注 计算平面图形面积时，总是要画该图形的概图，然后利用定积分或二重积分计算面积.

本题是综合题，其内容与计算方法见提高篇03，09.

（22）分析 （Ⅰ）由所给条件可知所给方程组对应的齐次线性方程组至少有两个线性无关的解，由此可得r（A）=2.

（Ⅱ）利用r（A）=2可确定a，b的值，将a，b的值代入所给方程组后计算通解.

精解 （Ⅰ）容易看到

r（A）≥2. （1）

此外，由于所给的非齐次线性方程组有三个线性无关的解，记为α₁，α₂，α₃，则α₁-α₂，α₁-α₃是对应的导出组（即齐次线性方程组）的解，并且它们线性无关，所以导出组的基础解系至少包含两个线性无关的解，由此知

r（A）≤4-2=2. （2）

由式（1）、式（2）得r（A）=2.

（Ⅱ）对A施行初等行变换

于是由r（A）=2得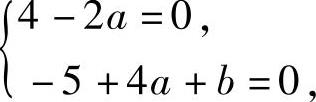即a=2，b=-3.

将以上算得的a，b值代入所给的非齐次线性方程组的增广矩阵A，并对A施行初等行变换得

由此可知，导出组有基础解系

（-2，1，1，0）^T，（4，-5，0，1）^T.此外，非齐次线性方程组有特解（2，-3，0，0）T，所以它的通解为

（x₁，x₂，x₃，x₄）^T=C₁（-2，1，1，0）^T+C₂（4，-5，0，1）^T+（2，-3，0，0）^T，

其中C₁，C₂是任意常数.

附注 有非零解的n元齐次线性方程组Ax=0的基础解系包含的解的个数r=n-r（A）.

由此可得

r（A）=n-r.

要熟记这一结论，并且要会正确地求解非齐次线性方程组Ax=b的通解.

本题是综合题，其有关内容与计算方法见提高篇16.

（23）分析 （Ⅰ）由题设可得A的特征值为λ=3，0（二重）及对应的特征向量.

精解 （Ⅰ）由于A的各行元素之和均为3，所以有

因此λ=3是A的特征值，它对应的所有特征向量为Cξ=C（1，1，1）T（其中C是任意非零常数）.

由于α₁，α₂是线性方程组Ax=0的两个解，所以有

Aα₁ =0·α₁， Aα₂=0·α_2.

因此，λ=0是A的（二重）特征值，其对应的所有特征向量为

C₁α₁+C₂α₂=C₁（-1，2，-1）^T+C₂（0，-1，1）^T（其中C₁，C₂是不全为零的任意常数）.

（Ⅱ）由（Ⅰ）可知，A有线性无关的特征向量ξ，α₁，α₂.为了计算Q，需将它们正交单位化.

正交化：由于ξ与α₁，α₂正交，所以只要将α₁，α₂正交化即可.

β₁=α₁ =（-1，2，-1）^T，

单位化：，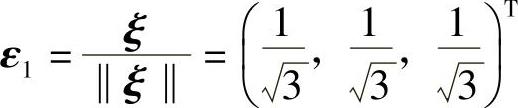

所以，所求的正交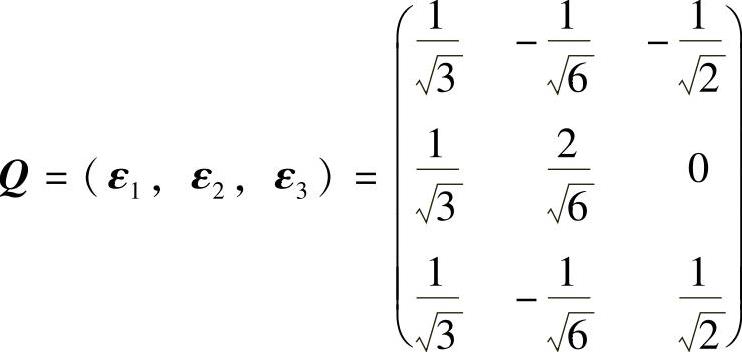矩阵，对角矩阵，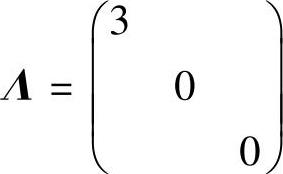

它们使得Q^TAQ=Λ成立.

附注 将题中的“向量α₁=（-1，2，1）^T和α₂=（0，-1，1）^T是线性方程组Ax=0的两个解”改成“η₁，η₂是线性方程组Ax=0的两个线性无关解”，同样可以解本题，实际上，只要利用η₁，η₂应与ξ=（1，1，1）^T正交即可.

本题是综合题，有关内容与计算方法见提高篇17，18.