一、选择题
(1)分析 从f(x)的零点入手考虑f′(x)的零点个数.
精解f(x)有三个不同的零点x=1,2和x=0(二重),故x=0必是f′(x)的零点.此外,由罗尔定理知,在(0,1)和(1,2)内f′(x)都有零点.所以三次多项式f′(x)有三个零点.
因此本题选(D).
附注 直接计算也可知选项(D)是正确的.
由f(x)=x4-3x3+2x2得
所以f′(x)确有三个零点.
(2)分析 先用分部积分法计算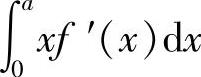 ,然后用定积分的几何意义确定正确的选项.
,然后用定积分的几何意义确定正确的选项.
精解
因此本题选(C).
附注 当f(x)≥0(x∈[a,b])时,
理解定积分的几何意义有时可快捷算得定积分,例如
当a>0时,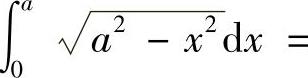 圆x2+y2≤a2面积的四分之一
圆x2+y2≤a2面积的四分之一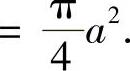
(3)分析 先利用常系数齐次线性微分方程的通解形式与其特征方程之间的一一对应关系写出特征方程,由此即可以判定正确的选项.
精解 对于三阶常系数齐次线性微分方程,当其有通解
y=C1ex+C2cos2x+C3sin2x
时,该微分方程的特征方程有特征根r=1,-2i和2i,所以特征方程为
(r-1)(r+2i)(r-2i)=0,即r3-r2+4r-4=0.
由此可得对应的微分方程为y‴-y″+4y′-4y=0.
因此本题选(D).
附注 应熟记二阶或三阶常系数齐次线性微分方程的特征方程与其通解形式之间存在的一一对应关系.
(4)分析 从函数f(x)的间断点入手判定正确选项.
精解f(x)有间断点x=0,1,由于
所以,点x=0是可去间断点,由于
所以,点x=1是跳跃间断点.
因此本题选(A).
附注 函数f(x)的间断点有两类,即第一类间断点和第二类间断点.
设点x0是f(x)的间断点,如果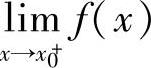 与
与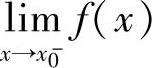 存在,则称点x0是f(x)的第一类间断点.特别地,当
存在,则称点x0是f(x)的第一类间断点.特别地,当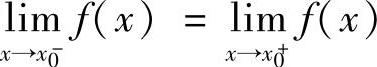 (此时
(此时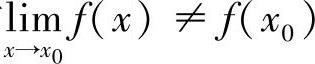 )时,称点x0是f(x)的可去间断点;当
)时,称点x0是f(x)的可去间断点;当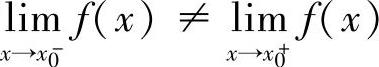 时,称点x0是f(x)的跳跃间断点.如果点x0不是f(x)的第一类间断点,则称点x0是f(x)的第二类间断点,特别地,当x→x0+或x→x0-时f(x)→∞,称点x0是f(x)的无穷间断点.
时,称点x0是f(x)的跳跃间断点.如果点x0不是f(x)的第一类间断点,则称点x0是f(x)的第二类间断点,特别地,当x→x0+或x→x0-时f(x)→∞,称点x0是f(x)的无穷间断点.
(5)分析 由于要考虑抽象数列的收敛性,并且其中有单调有界等条件,因此宜利用数列极限存在准则Ⅱ,判定正确选项.
精解 当{xn}单调时,由f(x)单调有界知数列{f(xn)}单调有界,因此由数列极限存在准则Ⅱ知{f(xn)}收敛.
因此本题选(B).
附注 数列极限存在准则Ⅱ是:
设数列{xn}单调不减有上界或单调不增有下界,则{xn}收敛.
(6)分析 用极坐标将F(u,v)表示成积分上限函数,然后计算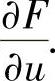
精解 设u>0,则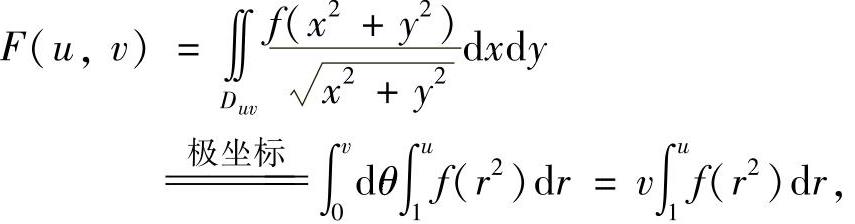
所以,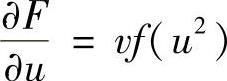 .由此可知,应排除选项(B)、(C)及(D).
.由此可知,应排除选项(B)、(C)及(D).
因此本题选(A).
附注 由于积分区域Duv是角域的一部分,且被积函数是x2+y2的函数,所以宜用极坐标计算所给的二重积分.
在计算中应注意u未必为正,如果不假定u>0,则有
显然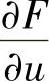 计算比较复杂.所以一开始假定u>0,由此排除三个选项,最后得正确选项.
计算比较复杂.所以一开始假定u>0,由此排除三个选项,最后得正确选项.
(7)分析 由A3=O,按可逆矩阵定义判定正确选项.
精解 由A3=O得E-A3=E.即(E-A)(E+A+A2)=E,所以E-A可逆.
由A3=O得E+A3=E,即(E+A)(E-A+A2)=E,所以E+A可逆.
因此本题选(C).
附注 本题也可从A的特征值入手求解:
设λ是A的特征值,则由A3=O知λ满足λ3=0,从而λ=0,即A的特征值全为零,因此E-A与E+A的特征值全为1.由此推得E-A与E+A都可逆.
(8)分析 利用实对称矩阵合同的充分必要条件是它们有相同个数的正特征值与负特征值,选择正确选项.
精解 由于|A|=-3<0,所以A的两个特征值中必一正一负.
由于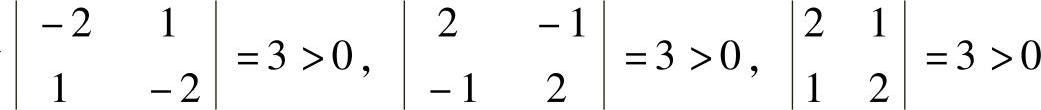 ,所以选项(A),(B),(C)的矩阵的特征值或全为正,或全为负,故A不可能与它们合同,应排除.
,所以选项(A),(B),(C)的矩阵的特征值或全为正,或全为负,故A不可能与它们合同,应排除.
因此本题选(D).
附注 记E是二阶单位矩阵,则
所以,选项(D)的矩阵特征值为λ=-1,3,确实是一正一负,因此A与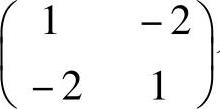 合同.
合同.
二、填空题
(9)分析 用等价无穷小代替算出极限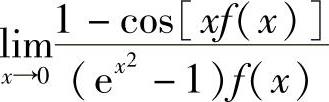 ,然后令它为1,算出f(0).
,然后令它为1,算出f(0).
精解 由于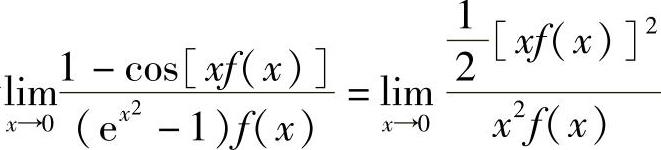
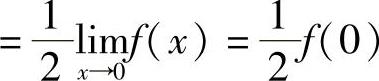 (利用f(x)在点x=0处连续),
(利用f(x)在点x=0处连续),
所以由题设得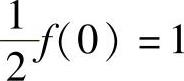 ,即f(0)=2.
,即f(0)=2.
附注 题解中利用了下列等价无穷小:x→0时,
(10)分析 改写所给的微分方程,使其成为某个函数的全微分,由此算出通解.
精解 所给微分方程可以改写成
ydx-xdy+x2e-xdx=0,即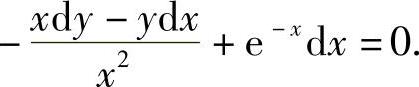
由此得到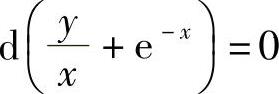 .所以通解为
.所以通解为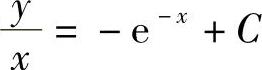 ,即y=-xe-x+Cx.
,即y=-xe-x+Cx.
附注 本题也可以解答如下:
所给微分方程可改写成
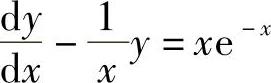 (一阶线性微分方程),
(一阶线性微分方程),
它的通解为
(11)分析 由隐函数求导算出y′(0),由此即可得到所求的切线方程.
精解 所给方程两边对x求导得
将x=0,y=1代入得 y′(0)=1.所以所求的切线方程为
y-1=1·(x-0),即y=x+1.
附注 关于曲线y=y(x)的切线方程的计算:
(ⅰ)当已知切点(x0,y0)(其中y0=y(x0))时,只要算出y′(x0)即得到切线方程
y-y0=y′(x0)(x-x0).
(ⅱ)当未知切点时,先根据所给条件算出切点,然后按(ⅰ)的方法写出切线方程.
(12)分析 计算y的二阶导数,确定y″的零点与使y″不存在的点,由此即可确定所给曲线的拐点.
精解 由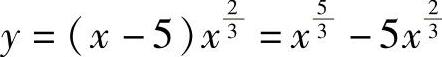 (其定义域为(-∞,+∞))得
(其定义域为(-∞,+∞))得
所以y″有零点x=-1,有不存在点x=0.据此列表如下:
由此可知,y″在点x=-1的两侧变号,所以点(-1,-6)是所给曲线的拐点;y″在点x=0的两侧不变号,所以(0,0)不是所给曲线的拐点.
因此所给曲线有唯一拐点(-1,-6).
附注 曲线y=f(x)的可能拐点横坐标来自其定义域内的以下两种点:
(ⅰ)f″(x)的零点;
(ⅱ)使f″(x)不存在的点.
(13)分析 记φ(x)=z(x,2),则由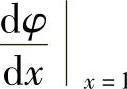 即得
即得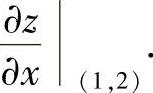
精解 由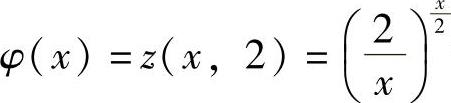 得
得
上式两边对x求导得
将x=1, 代入上式得
代入上式得
从而 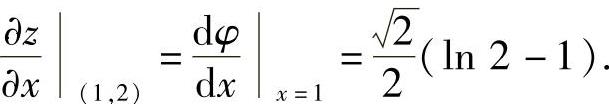
附注 顺便计算 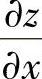 与
与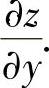
记 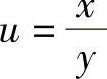 ,则z=u-u,即lnz=-ulnu.
,则z=u-u,即lnz=-ulnu.
上式两边求微分得
从而 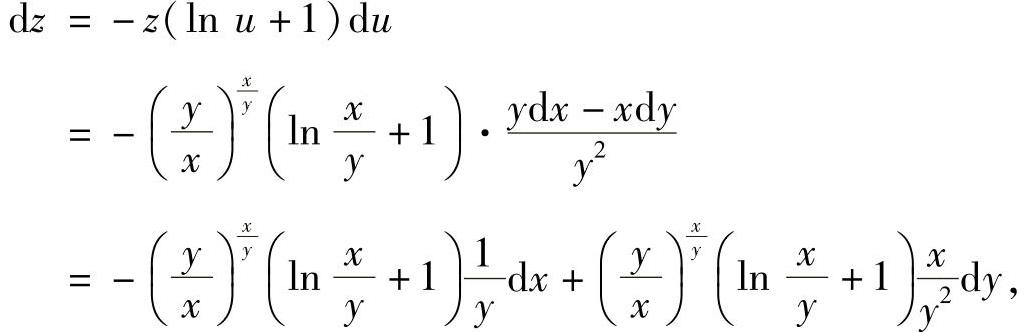 (https://www.xing528.com)
(https://www.xing528.com)
所以 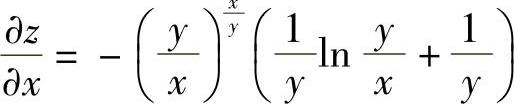 ,
,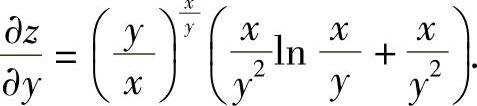
(14)分析 利用矩阵的行列式的性质即得到λ的值.
精解 由于|2A|=23|A|=8×2×3×λ=48λ,所以由题设得
48λ=-48,即λ=-1.
附注 应记住以下常用的结论:
设A是n阶矩阵,则
|kA|=kn|A|(k是常数),
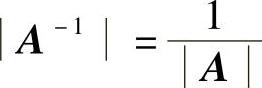 (当A可逆时),
(当A可逆时),
|A|=λ1λ2…λn(其中λ1,λ2,…,λn是A的n个特征值).
三、解答题
(15)分析 所给极限是 型未定式,用等价无穷小代替进行求解.
型未定式,用等价无穷小代替进行求解.
精解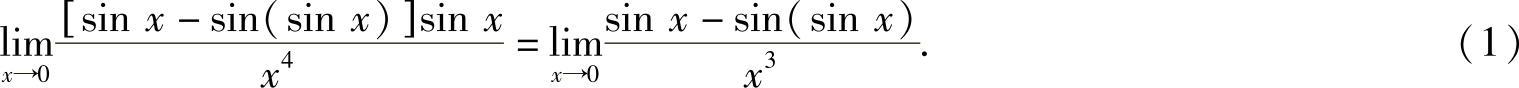
由于 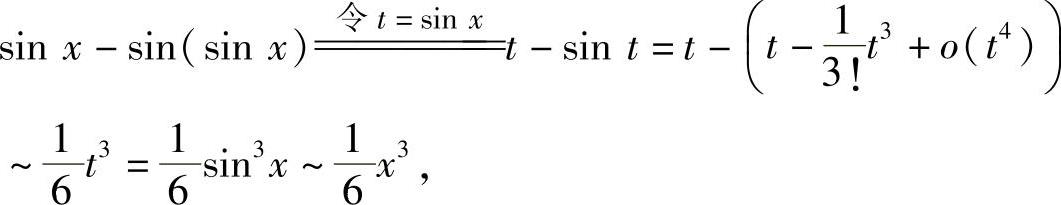
所以 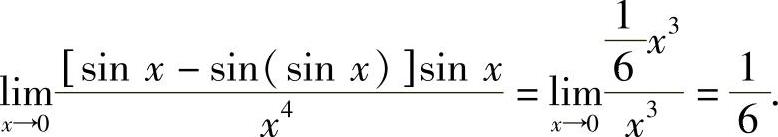
附注 (ⅰ)式(1)右边极限也可使用洛必达法则计算:
(ⅱ)本题的计算方法见提高篇01.
(16)分析 先算出x(t)的表达式,然后按对参数方程表示的函数求二阶导数的方法计算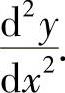
精解 由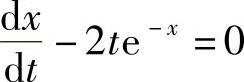 得exdx=2tdt.
得exdx=2tdt.
上式两边积分得 ex=t2+C.利用x|t=0=0得1=0+C,即C=1.所以
ex=1+t2,即x=ln(1+t2).
因此,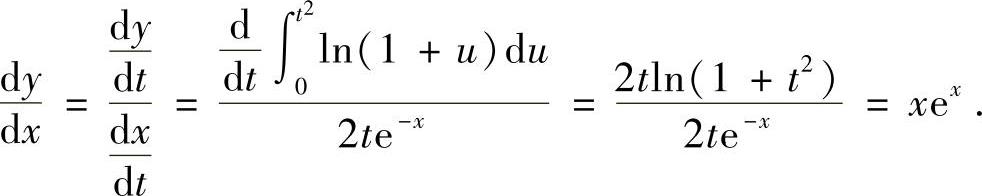
由此得到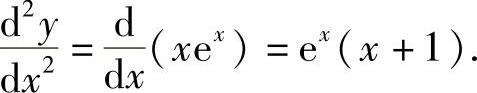
附注 (ⅰ)题解中,将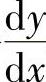 表示为
表示为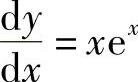 ,这样便于计算
,这样便于计算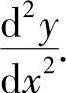
(ⅱ)本题是综合题,其有关内容及计算方法见提高篇03,13.
(17)分析 作变量代换t=arcsinx后,用分部积分法计算所给的定积分.
精解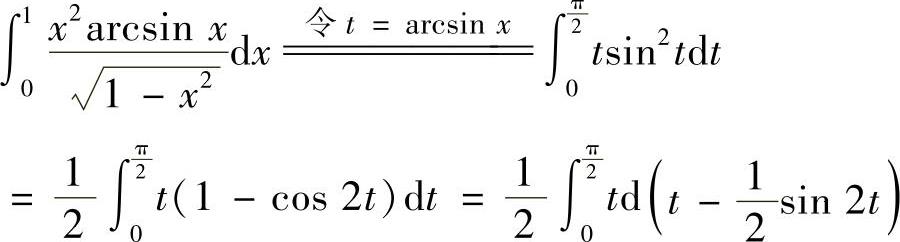
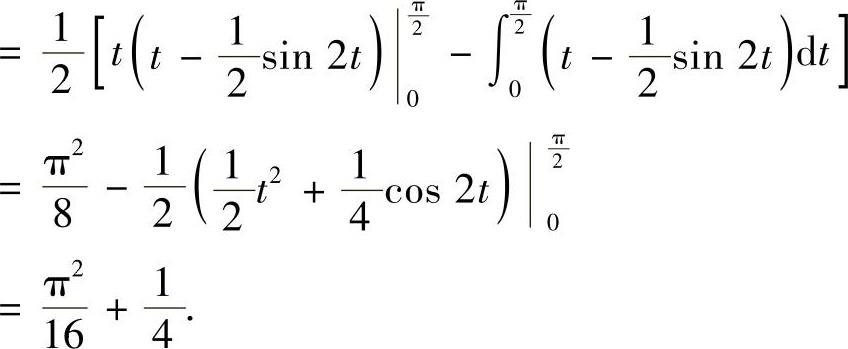
附注 换元积分法与分部积分法是定积分计算的两种基本方法.通常,根据所求定积分的特点将它们结合起来使用,更有效地计算定积分.
(18)分析 将D用曲线xy=1划成两块,然后计算二重积分.
图 B-08-1
精解 将D用曲线xy=1划分成D1与D2,如图B-08-1所示,则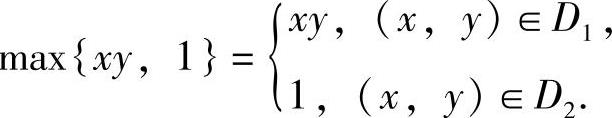 所以
所以
附注 将 转换成
转换成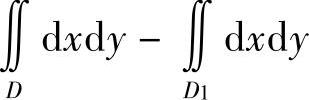 ,使计算简单些.
,使计算简单些.
有关分块函数的二重积分计算,见提高篇12.
(19)分析 写出旋转体侧面积和体积的积分表达式,据此按题意建立方程,求导后转换成微分方程.解此微分方程求得函数f(x)的表达式.
精解 旋转体侧面积为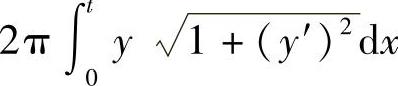 ,旋转体的体积为
,旋转体的体积为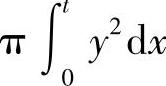 ,所以由题设得方程
,所以由题设得方程
上式两边对t求导得
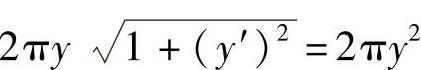 ,即
,即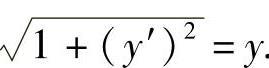
解出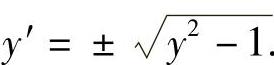 根号前取负号不符合y=f(x)是单调增加函数的假定,所以
根号前取负号不符合y=f(x)是单调增加函数的假定,所以
上式两边积分得
令x→0+对式(1)两边取极限,并将 代入得C=0.将它代入式(1)得
代入得C=0.将它代入式(1)得
解出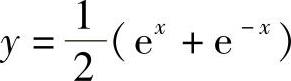 .因此所求的函数为
.因此所求的函数为
附注 平面区域D={(x,y)a≤x≤b,0≤y≤f(x)}绕x轴旋转一周而成的旋转体体积为
而该旋转体的侧面积为
应熟记这两个公式.
本题是综合题,其有关内容与计算方法见提高篇09,13.
(20)分析 (Ⅰ)利用连续函数在闭区间上的性质证明积分中值定理.
(Ⅱ)先由积分中值定理确定η∈(2,3],使得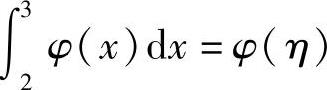 .然后在[1,2]和[2,η]上分别应用拉格朗日中值定理,得到ξ1∈(1,2),ξ2∈(2,η),最后再在[ξ1,ξ2]上应用拉格朗日中值定理即可.
.然后在[1,2]和[2,η]上分别应用拉格朗日中值定理,得到ξ1∈(1,2),ξ2∈(2,η),最后再在[ξ1,ξ2]上应用拉格朗日中值定理即可.
精解 (Ⅰ)由于函数f(x)在[a,b]上连续,所以有最小值m和最大值M,因此
即 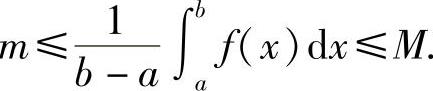
于是,由连续函数介值定理知,存在η∈[a,b],使得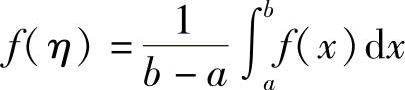 ,即
,即
(Ⅱ)由积分中值定理知,存在η∈[2,3],使得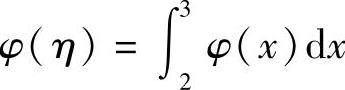 .由于φ(2)>
.由于φ(2)>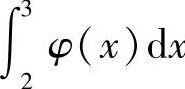 ,即φ(2)>φ(η),所以η≠2,从而上述的η∈(2,3].
,即φ(2)>φ(η),所以η≠2,从而上述的η∈(2,3].
由于函数φ(x)可导,所以可在[1,2]和[2,η]上对φ(x)分别应用拉格朗日中值定理,故存在ξ1∈(1,2)和ξ2∈(2,η),使得
φ(2)-φ(1)=φ′(ξ1)(2-1),φ(η)-φ(2)=φ′(ξ2)(η-2),
由此得到 φ′(ξ1)>0,φ′(ξ2)<0. (1)
由于φ′(x)可导,所以可在[ξ1,ξ2]上对φ′(x)应用拉格朗日中值定理,故存在ξ∈(ξ1,ξ2)⊂(1,3),使得
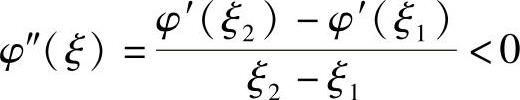 (利用式(1)).
(利用式(1)).
附注 (ⅰ)从本题(Ⅰ)可以看到,对一些重要定理的证明应掌握.
(ⅱ)当问题的条件或结论中出现定积分时,往往用积分中值定理将其改造成不带定积分的形式,故本题将条件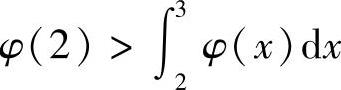 改造成φ(2)>φ(η).
改造成φ(2)>φ(η).
本题是综合题,有关内容与计算方法见提高篇04.
(21)分析 用拉格朗日乘数法计算u在约束条件下的最大值与最小值.
精解 作拉格朗日函数
F(x,y,z)=x2+y2+z2+λ(x2+y2-z)+μ(x+y+z-4),
并且 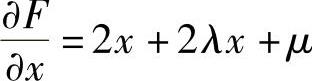 ,
,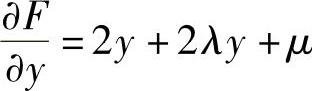 ,
,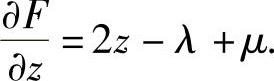 于是由拉格朗日乘数法得
于是由拉格朗日乘数法得
由式(1)、式(2)知x=y.将它代入式(4)与式(5)得
消去z得 x2+x-2=0.所以x=-2,1,对应地有y=-2,1,z=8,2.
容易知道,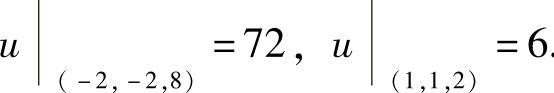 所以u在约束条件下的最大值与最小值分别为72与6.
所以u在约束条件下的最大值与最小值分别为72与6.
附注 应熟练掌握用拉格朗日乘数法计算二、三元函数在约束条件下的最值的方法.
(22)分析 (Ⅰ)利用行列式性质将|A|化为上三角形行列式后算出|A|.
(Ⅱ)由|A|≠0算出Ax=b有唯一解的a值,并由克莱姆法则算出x1.
(Ⅲ)由|A|=0算出Ax=b有无穷多解的a值.将求得的a值代入Ax=b即可得到通解.
精解 (Ⅰ)
(Ⅱ)当a≠0时,|A|≠0,所以此时方程组Ax=b有唯一解,且由克莱姆法则得
其中 
将式(2)代入式(1)得
(Ⅲ)当a=0时,方程组Ax=b成为
它即为方程组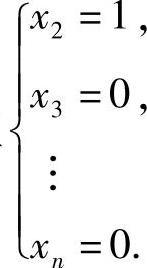 由此可知,x1可任意取值,所以方程组(3)有无穷多解,其通解为
由此可知,x1可任意取值,所以方程组(3)有无穷多解,其通解为 (其中c是任意常数).
(其中c是任意常数).
附注n阶行列式Dn通常有两种计算方法:利用行列式性质将Dn化为三角形行列式;按一行或一列展开Dn.应熟练地掌握三阶行列式及简单的n(n>3)阶行列式的计算.
(23)分析 (Ⅰ)用定义证明α1,α2,α3线性无关.
(Ⅱ)利用α1,α2都是A的特征向量及Aα3=α2+α3可以得A(α1,α2,α3)=(α1,α2,α3)B,由此算得B=P-1AP.
精解 (Ⅰ)设有数k1,k2,k3,使得
k1α1+k2α2+k3α3=0. (1)
于是有 A(k1α1+k2α2+k3α3)=0,即k1Aα1+k2Aα2+k3Aα3=0,
将Aα1=-α1,Aα2=α2(因为α1,α2是A的对应特征值为-1,1的特征向量),Aα3=α2+α3代入上式得
-k1α1+k2α2+k3(α2+α3)=0,即-k1α1+(k2+k3)α2+k3α3=0. (2)
式(1)-式(2)得 2k1α1-k3α2=0. (3)
由于α1,α2是A的属于不同特征值的特征向量,所以线性无关,从而由式(3)得k1=k3=0.将它们代入式(1)得 k2α2=0.由于α2是A的特征向量,不为零向量,所以k2=0.
因此要使式(1)成立,必须k1=k2=k3=0.由此推得α1,α2,α3线性无关.
(Ⅱ)由α1,α2,α3线性无关知,矩阵P=(α1,α2,α3)可逆,且
所以 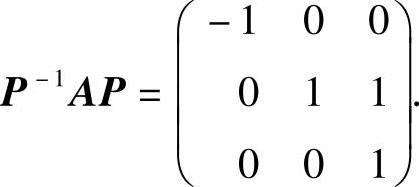
附注 由题解可知,A是不可相似对角化的.这是因为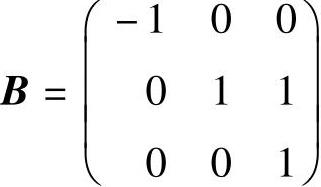 有特征值λ=-1和λ=1(二重),但n-2=3-2≠r(1·E-B)=2(其中E是三阶单位矩阵),所以B不可相似对角化.
有特征值λ=-1和λ=1(二重),但n-2=3-2≠r(1·E-B)=2(其中E是三阶单位矩阵),所以B不可相似对角化.
本题是综合题,其有关内容及计算方法见提高篇17.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




